Full Small-Change Problem

Now that we understand how things hang together, let's do the full problem.

Let's first put our original system of equations

in differential form:

(h_p and are the partial derivatives of ; I am no longer assuming a perfect gas, so I do not know what they are.)

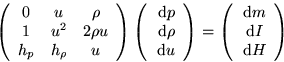
Since all shocks have m, I, and H the same at both sides of the shock, weak shocks are nonzero solutions to the homogeneous system above. So for weak shocks to occur, the determinant of the matrix must be zero.

And zero determinant is exactly the condition in which the inhomogeneous system is not normally solvable, indicating that the flow is choked: there is normally no solution for further changes .

When is the determinant zero? Well, we already answered it in the section on weak shocks in the ``Normal Shocks'' handout. But let's do it again, this time using the determinant, which multiplies out to

or

Since

it is seen that and , so

with the final equality from the well known calculus rule.

By the definition of the speed of sound, it follows that our weak shocks, as well as our choking problems appear when

u² = a²

i.e. when the flow is sonic.