Expansion and compression shocks

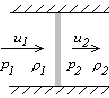
The interesting thing about our three equations (1-3) is that if they are satisfied for states 1 and 2, they are still satisfied if you flip around the velocity vectors, i.e. if you replace u₁ by -u₁ and u₂ by -u₂. (Check this.) So for any shock that looks like this:

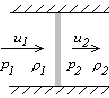
there is also a shock that looks like this:

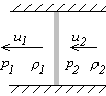
In one case the fluid density changes from to when the fluid moves across the shock, while in the other case it changes from into . So, the fluid will change from low density to high density in one of the two flows above, and from high to low density in the other. The one in which the fluid density increases is called the ``compression shock'' since the fluid is being compressed, and the other the ``expansion shock'', since the fluid expands. So we have learned:

• For any compression shock, there is a corresponding expansion shock. And vice versa.

Note however that while all conservation laws are satisfied, there is still a problem with the second law of thermodynamics. Depending on which side, 1 or 2, has the higher entropy, the fluid in one case increases in entropy while going through the shock, and in the other decreases in entropy. Since the shock is adiabatic, entropy cannot decrease according to the second law. It follows that:

• Either the compression shock or the expansion shock can occur in nature, not both.

It turns out (from results obtained later) that it is the compression shock that has an entropy that is correctly increasing, so

• The expansion shocks cannot occur in nature. The compression shocks are OK.

(Note that this is true for a perfect gas such as normal air. I do not know a proof myself that it is true for any gas. If you know such a proof, or a counter example, let me know.)

From continuity, (1), is constant, so if density increases, the velocity decreases:

• The fluid slows down over physical shocks.

You more or less expect that kinetic energy would decrease due to friction; however, the second law only says that entropy increases, not that kinetic energy decreases.

So far for what can be seen immediately. Let's now start solving the three equations to see what more we can learn there.