Solution stage 1

To solve three nonlinear equations in three unknowns, you will typically try to use one of the equations to get rid of one of the three unknowns in the other two equations. This then leaves you with two equations in the two remaining unknowns. Repeat the trick and you are left with one equation in one unknown. That one may be solvable.

Here, let us use the continuity equation (1), the simplest equation, to get rid of the velocity u₂ from the momentum and energy equations (2) and (3). That will leave those two equations with only the two thermodynamic unknowns p₂ and .According to continuity, . Put it into (2) to get

Let's bring the remaining velocity u₁ to one side and all the thermodynamic stuff to the other side:

In the same way, use continuity to get rid of u₂ in the energy equation (3):

In addition we can use (2') to also get rid of u₁² and thus have only thermo stuff left. If we do that, cleaning up as much as possible, we get (check this):

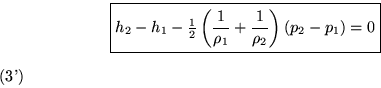
Each of our two reduced equations is a fountain of further information, especially about the behavior of weak shocks