Weak shocks

Weak shocks are shocks across which the differences in velocity, pressure, and density are all very small. We can then approximate as , , , , etcetera.

Starting with (3'), it becomes:

but that is just ! We see:

• Weak shocks are almost isentropic (reversible).

This is the justification why some computational schemes for transsonic flow ignore the irreversibility effects. But note that this can be tricky. If you raise the velocity of a sphere in an inviscid fluid enough to create a small supersonic pocket around it, the total pressure loss of the fluid going through the shock is enough to prevent it from reaching the rear symmetry plane. That would not be correctly seen in a computation in which irreversibility is ignored.

Our other equation, (2') is even more interesting for weak shocks. It becomes:

Since, according to (3' weak), the entropy is constant across the weak shock, the ratio of the pressure difference over the density difference became the partial derivative of pressure with respect to density keeping the entropy s constant.

Now, looking again at the picture, u₁ is the velocity of the shock compared to the fluid entering the shock:

In other words, compared to the fluid, the weak shock is moving with a relative speed a given by:

This speed a is called the ``speed of sound''. So:

• weak shocks move through a gas with the speed of sound a given by the formula above.

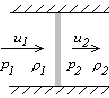
In fact, not only weak shocks, but also other weak disturbances in a gas move with the speed of sound. That is because a disturbance (or ``wave'') can be approximated as a lot of small shocks; for example, this is shown for the pressure profile below:

The true profile is in black and the approximation by a series of weak shocks is shown in grey. Of course, if the direction of flow in the figure would be towards the left, the approximating shocks will be expansion shocks, but since weak shocks are isentropic, that is no problem. We see:

• Small disturbances move through a gas with the speed of sound a given by the formula above.

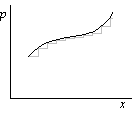
That closes the observations about weak shocks. Back to finite strength ones. We now want to complete the solution process.