Solution stage 2

In the previous section we derived two equations (2') and (3') for the two unknowns p₂ and behind the shock:

Now we want to use (2') to eliminate p₂ from (3'). The resulting equation (3'') then only contains the unknown and we can solve it for . Knowing , it will be easy to figure out the other unknowns behind the shock.

It is easy to solve (2') for p₂ in terms of the other parameters:

and if we substitute that in (3'), we have our equation involving only the unknown .

However, a difficulty arises. Unless we know what sort of function the enthalpy is, there is no way to solve (3') for .So, here is where we need to restrict ourselves to a perfect gas. While our results so far were all valid for any gas, from now on the results will only apply to perfect gasses.

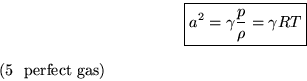
First, for a perfect gas, the speed of sound becomes particularly simple. We know that when the entropy is constant for a perfect gas, , so

hence:

Or in words, the speed of sound is simply a constant times the square root of the temperature. That was first discovered by Newton, although he had the constant wrong. He missed the .

Again for a perfect gas, the enthalpy is easily found as

or dividing top and bottom by c_v:

Note that enthalpy, temperature, and square speed of sound are all proportional to each other.

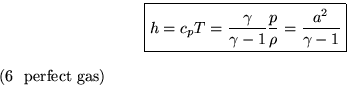
Replacing h in (3') with the second expression in (6), and substituting in p₂ from (2'), we will get a solvable equation for .

But, again, before grinding anything out, let's think first. Let's first see what we can expect for our solution based on dimensional analysis.