Full solution

As announced, we now substitute p₂ from (2'),

into (3'), using the enthalpy formula (6),

Nondimensionalize by dividing by and you get a quadratic equation for . Divide out the common factor corresponding to the trivial solution , and you get a linear equation which gives the final result:

(The density ratio across the shock is the inverse of the velocity ratio because of the continuity equation (1).)

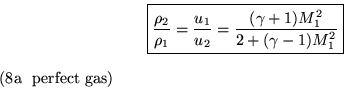
Next, plug the above result for the density ratio into the equation (2') and you have p₂. The result is rather simple after clean-up:

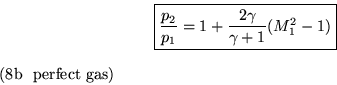
The entropy difference across the shock can be found by taking the familiar combination of logarithms of the ratios (8a) and (8b).

Since , if you take the ratio of (8b) over (8a), you get T₂/T₁, which is also equal to the ratio h₂/h₁ and to (a₂/a₁)². Since the formulae do not simplify any further, we will skip writing it down.

You can get the Mach number M₂ behind the shock by noting that it is M₁ (u₂/u₁) / (a₂/a₁), where the two ratios have already been found. From static quantities and the just found Mach number M₂, you can find stagnation quantities behind the shock and so on.

All done, except for examining some results a bit closer.