Examination of some results

To assist in examining the results in more depth, let's digress a bit and think about what are stagnation and what are critical quantities. Stagnation, or total, quantities are the quantities you get when you bring the fluid isentropically to a halt. For example, the stagnation pressure is the pressure when the fluid has been brought to a halt, and the stagnation enthalpy is the corresponding enthalpy.

A formula for the stagnation enthalpy can be found from energy conservation for the isentropic process, which says that constant:

This important relationship can be written in nondimensional form by dividing by h, and using to get the result in terms of the Mach number:

where we also used the fact that enthalpy, temperature, and square speed of sound are all proportional, (6), so that their ratios are equal.

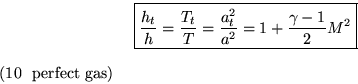
The energy equation (3) ensures that the stagnation enthalpy remains constant across a shock. It follows that the stagnation temperature T_t and stagnation speed of sound are then the same at both sides too.

On the other hand, the familiar expressions for the entropy,

show that if the entropy increases across the shock, and the ratio of total temperatures is unity, then the ratio of total pressures, as well as the ratio of total densities must be less than one:

• total pressure and total density decrease over shock waves. (Even though pressure and density themselves increase.)

Just like stagnation quantities are the values you get when you bring the fluid isentropically to a stop, ``critical'' quantities are the values you get when you bring the fluid isentropically to a unit Mach number. In particular, by definition the critical velocity V^* equals the critical speed of sound a^*.

Since the Mach number is unity at the critical condition, (10) implies that stagnation speed of sound a_t and the critical speed of sound a^* differ by only a constant:

Since we already know that the stagnation speed of sound is the same at both sides of the shock, the critical speed of sound must therefor also be the same.

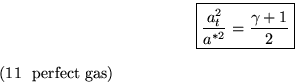
That is nice, since it allows us to define a new Mach number, M^* using the critical instead of the local speed of sound:

Since the critical speed of sound is the same at both sides, the new Mach number M^* is a direct measure for the velocity. In contrast, the normal Mach number varies both due to changes in the velocity and due to variations in the local speed of sound.

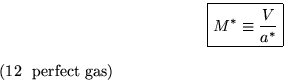
The relationship between M^* and M is easy; just correct for the speed of sound:

Both speed of sound ratios in this expression we already wrote down in (10) and (11). If we substitute them in, we get:

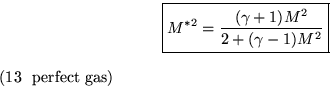
To find the Mach number M₂^* behind the shock is supereasy if we remember that this Mach number is directly proportional to the velocity, so M₁^*/M₂^*=u₁/u₂, and that ratio we already found in (8a). But look at the right hand side in (8a): it happens to be equal to M₁^*2, see (13)!

So M₁^*/M₂^*=M₁^*2 or:

This beautifully simple formula is called the Prandtl relation. It implies that one side of a steady normal shock will be supersonic, and the other side subsonic.

Let's define side 1 to be the supersonic side and side 2 subsonic, i.e. M₁^*>1. According to (14), the density is higher at side 2 and according to (8b), so is the pressure. The velocity is lower at side 2, which implies that the temperature too is higher at side 2 since the total enthalpy is the same.

Further, a careful examination of the entropy shows that the entropy is higher at side 2, so the fluid is flowing from 1 to 2. That implies the already mentioned property that only compression shocks, in which the fluid is compressed, are physical:

• when fluid passes through a shock wave, it goes to higher pressure, higher density, higher temperature, higher enthalpy, and higher entropy.

Also note that from (10) that the Mach number M₁^* is bounded; it has a limit of for infinite Mach number M₁. (This reflects that kinetic energy, hence velocity, is bounded by the available total enthalpy. And M^* is proportional to the velocity. The normal Mach number M can approach infinity in a flow not because the velocity goes to infinity, but because the speed of sound goes to zero.) But if M₁^* has a largest value, the Prandtl relation shows that M₂^* will have a nonzero smallest value, and so will M₂. So:

• the Mach number behind a shock will not go below a certain minimum value, even if the upstream Mach number tends to infinity.