Next: Full solution
Up: Solution stage 2
Previous: Solution stage 2
Remember from your undergraduate fluids that if we have a relationship
of the form
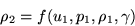
then the nondimensional ratio 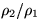 will be a function of
the nondimensional combinations (or
will be a function of
the nondimensional combinations (or 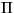 -groups) that we can make
from the four function arguments. Now
-groups) that we can make
from the four function arguments. Now 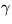 is already a
nondimensional number. From the other three, we can only get rid of
the mass dimension by taking the ratio
is already a
nondimensional number. From the other three, we can only get rid of
the mass dimension by taking the ratio 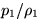 , which we already
know is proportional to the speed of sound a1. We can then get rid
of the velocity dimension by taking a ratio with the speed u1. So
our only other nondimensional combination is the Mach number M1=u1/a1,
and dimensional analysis then tells us that
, which we already
know is proportional to the speed of sound a1. We can then get rid
of the velocity dimension by taking a ratio with the speed u1. So
our only other nondimensional combination is the Mach number M1=u1/a1,
and dimensional analysis then tells us that

Of course, the same holds for any other nondimensional ratio we solve
for. So the form of our solution will be:
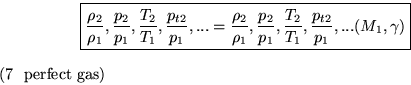
For the important case of normal air, i.e. 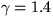 , the book
provides all these functions in tabular form in Table A.2.
The first column in the table is the Mach number M1, the second column the
corresponding p2/p1, the third
, the book
provides all these functions in tabular form in Table A.2.
The first column in the table is the Mach number M1, the second column the
corresponding p2/p1, the third 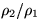 , etcetera.
, etcetera.
For other values of 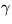 than 1.4, you will have to use the
actual formulae, which we will derive now.
than 1.4, you will have to use the
actual formulae, which we will derive now.
Next: Full solution
Up: Solution stage 2
Previous: Solution stage 2
![]()
![]()
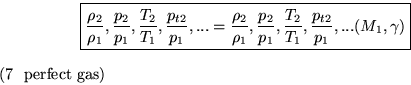
![]() , the book
provides all these functions in tabular form in Table A.2.
The first column in the table is the Mach number M1, the second column the
corresponding p2/p1, the third
, the book
provides all these functions in tabular form in Table A.2.
The first column in the table is the Mach number M1, the second column the
corresponding p2/p1, the third ![]() , etcetera.
, etcetera.
![]() than 1.4, you will have to use the
actual formulae, which we will derive now.
than 1.4, you will have to use the
actual formulae, which we will derive now.