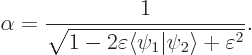| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
5.3.1 Solution 2state-a
Question:
The effectiveness of mixing states was already shown by the hydrogen molecule and molecular ion examples. But the generalized story above restricts the basis
states to be orthogonal, and the states used in the hydrogen examples were not.
Show that if 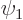 and
and 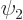 are not orthogonal states, but are normalized and produce a real and positive value for
are not orthogonal states, but are normalized and produce a real and positive value for 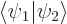 , like in the hydrogen examples, then orthogonal states can be found in the form
, like in the hydrogen examples, then orthogonal states can be found in the form
For normalized 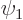 and
and 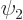 the Cauchy-Schwartz inequality implies that
the Cauchy-Schwartz inequality implies that 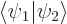 will be less than one. If the states do not overlap much, it will be much less than one and
will be less than one. If the states do not overlap much, it will be much less than one and 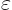 will be small.
will be small.
(If 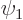 and
and 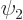 do not meet the stated requirements, you can always redefine them by factors
do not meet the stated requirements, you can always redefine them by factors 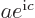 and
and 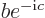 , with
, with 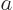 ,
, 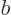 , and
, and 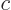 real, to get states that do.)
real, to get states that do.)
Answer:
The inner product of 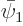 and
and 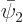 must be zero for them to be orthogonal:
must be zero for them to be orthogonal:
and this can be multiplied out, dropping the common factor 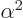 and noting that
and noting that 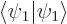 and
and 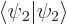 are one, as
are one, as
for which the smallest root can be written as
That is less than 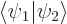 , hence
, hence 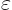 is small if the overlap is small.
is small if the overlap is small.
The constant 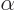 follows from the requirement that the new states must still be normalized, and is found to be
follows from the requirement that the new states must still be normalized, and is found to be
Note that the denominator is nonzero; the argument of the square root exceeds 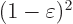 .
.
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
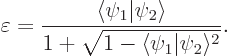
![]()