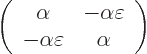| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
5.3.2 Solution 2state-b
Question:
Show that it does not have an effect on the solution whether or not the basic states 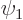 and
and 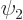 are normalized, like in the previous question, before the state of lowest energy is found.
are normalized, like in the previous question, before the state of lowest energy is found.
This requires no detailed analysis; just check that the same solution can be described using the nonorthogonal and orthogonal basis states. It is however an important observation for various numerical solution procedures: your set of basis functions can be cleaned up and simplified without affecting the solution you get.
Answer:
Using the original basis states, the solution, say the ground state of lowest energy, can be written in the form
for some values of the constants 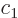 and
and 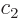 . Now the expression for the orthogonalized functions,
. Now the expression for the orthogonalized functions,
can for given 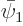 and
and 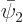 be thought of as two equations for
be thought of as two equations for 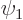 and
and 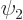 that can be solved. In particular, adding
that can be solved. In particular, adding 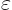 times the second equation to the first gives
times the second equation to the first gives
Similarly, adding 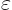 times the first equation to the second gives
times the first equation to the second gives
If this is plugged into the expression for the solution, 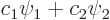 , it takes the form
, it takes the form
where
So, while the constants 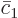 and
and 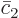 are different from
are different from 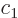 and
and 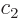 , the same solution can be found equally well in terms of
, the same solution can be found equally well in terms of 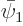 and
and 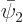 as in terms of
as in terms of 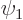 and
and 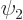 .
.
In the terms of linear algebra, 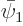 and
and 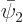
span the same function space
as 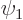 and
and 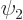 : any wave function that can be described as a combination of
: any wave function that can be described as a combination of 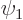 and
and 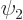 can also be described in terms of
can also be described in terms of 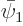 and
and 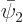 , although with different constants. This is true as long as the definitions of the new functions can be solved for the old functions as above. The matrix of coefficients, here
, although with different constants. This is true as long as the definitions of the new functions can be solved for the old functions as above. The matrix of coefficients, here
must have a nonzero determinant.
![]()
![]()
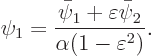
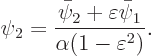
![]()
![]()
![]()
![]() :
:![]()
![]()
![]()
![]() ,
,