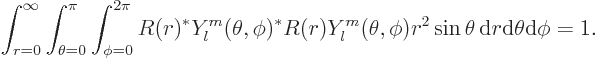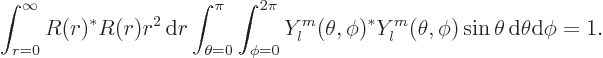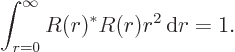| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.2.3.1 Solution anguc-a
Question:
The general wave function of a state with azimuthal quantum number 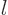 and magnetic quantum number
and magnetic quantum number 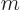 is
is 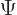

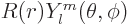 , where
, where 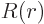 is some further arbitrary function of
is some further arbitrary function of 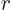 . Show that the condition for this wave function to be normalized, so that the total probability of finding the particle integrated over all possible positions is one, is that
. Show that the condition for this wave function to be normalized, so that the total probability of finding the particle integrated over all possible positions is one, is that
Answer:
You need to have 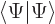

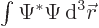
 1 for the wave function to be normalized. Now the volume element
1 for the wave function to be normalized. Now the volume element 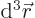 is in spherical coordinates given by
is in spherical coordinates given by 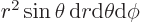 , so you must have
, so you must have
Taking this apart into two separate integrals:
The second integral is one on account of the normalization of the spherical harmonics, so you must have
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() .
.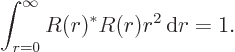
![]()
![]()
![]()
![]()
![]()
![]() ,
,