| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.2.3.2 Solution anguc-b
Question:
Can you invert the statement about zero angular momentum and say: if a particle can be found at all angular positions compared to the origin with equal probability, it will have zero angular momentum?
Answer:
No. To be at zero angular momentum, not just the probability 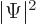 , but
, but 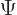 itself must be independent of the spherical coordinate angles
itself must be independent of the spherical coordinate angles 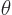 and
and 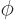 . As an arbitrary example,
. As an arbitrary example, 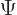

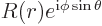 would have a probability of finding the particle independent of
would have a probability of finding the particle independent of 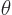 and
and 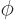 , but not zero angular momentum.
, but not zero angular momentum.
![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,