5.5.2.1 So­lu­tion com­plex­sai-a

Ques­tion:

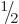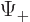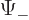Show that the nor­mal­iza­tion re­quire­ment for the wave func­tion of a spin $\leavevmode \kern.03em\raise.7ex\hbox{\the\scriptfont0 1}\kern-.2em /\kern-.21em\lower.56ex\hbox{\the\scriptfont0 2}\kern.05em$ par­ti­cle in terms of $\Psi_+$ and $\Psi_-$ re­quires its norm 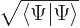$\sqrt{\langle\Psi\vert\Psi\rangle}$ to be one.

An­swer:

As a cor­re­spond­ing ques­tion in the pre­vi­ous sub­sec­tion dis­cussed; the to­tal prob­a­bil­ity of find­ing the par­ti­cle some­where with spin up is 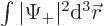$\int\vert\Psi_+\vert^2{\rm d}^3{\skew0\vec r}$, and the to­tal prob­a­bil­ity of find­ing it some­where with spin down is 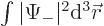$\int\vert\Psi_-\vert^2{\rm d}^3{\skew0\vec r}$. The sum of the two in­te­grals must be one to ex­press the fact that the prob­a­bil­ity of find­ing the par­ti­cle some­where, ei­ther with spin up or spin down, must be one, cer­tainty.

Com­pare that with the square norm of the wave func­tion, which is by de­f­i­n­i­tion the in­ner prod­uct of the wave func­tion with it­self:

$$\langle\Psi\vert\Psi\rangle = \langle\Psi_+{\uparrow}+ \Psi_... ...ngle\Psi_+\vert\Psi_+\rangle + \langle\Psi_-\vert\Psi_-\rangle$$

and the fi­nal two in­ner prod­ucts are by de­f­i­n­i­tion the two in­te­grals above. Since their sum must be one, it fol­lows that the norm of the wave func­tion 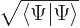$\sqrt{\langle\Psi\vert\Psi\rangle}$ must be one even if there is spin.