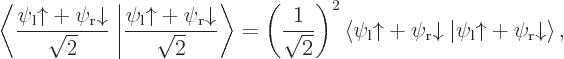| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
5.5.2.2 Solution complexsai-b
Question:
Assume that 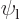 and
and 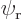 are normalized spatial wave functions. Now show that a combination of the two like
are normalized spatial wave functions. Now show that a combination of the two like 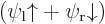
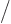
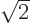 is a normalized wave function with spin.
is a normalized wave function with spin.
Answer:
You have
and multiplying out the inner product according to the rule spin-up components together and spin-down components together,
and since it is given that 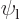 and
and 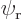 are normalized
are normalized
![]()
![]()
![]()
![]()
![]()