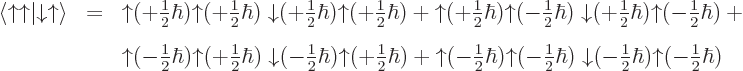| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
5.5.4.1 Solution complexsb-a
Question:
As an example of the orthonormality of the two-particle spin states, verify that 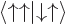 is zero, so that
is zero, so that 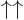 and
and 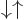 are indeed orthogonal. Do so by explicitly writing out the sums over
are indeed orthogonal. Do so by explicitly writing out the sums over 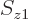 and
and 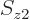 .
.
Answer:
The inner product is by definition
or writing out the second sum explicitly
or writing out the first sum also explicitly
and noting that 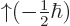
 0 and
0 and 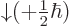
 0, you see that all terms are zero.
0, you see that all terms are zero.
![]()
![]()
![]()
![]()
![]() .
.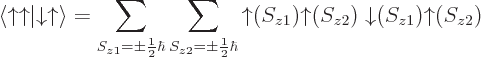
![\begin{displaymath}
\langle{\uparrow}{\uparrow}\vert{\downarrow}{\uparrow}\rangl...
...rrow}(S_{z1}){\uparrow}(-{\textstyle\frac{1}{2}}\hbar) \right]
\end{displaymath}](img532.gif)