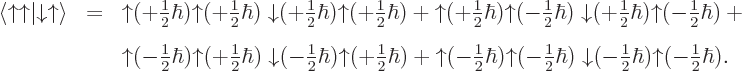| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
5.5.4.2 Solution complexsb-b
Question:
A more concise way of understanding the orthonormality of the two-particle spin states is to note that an inner product like 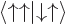 equals
equals 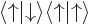 , where the first inner product refers to the spin states of particle 1 and the second to those of particle 2. The first inner product is zero because of the orthogonality of
, where the first inner product refers to the spin states of particle 1 and the second to those of particle 2. The first inner product is zero because of the orthogonality of 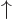 and
and 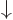 , making
, making 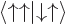 zero too.
zero too.
To check this argument, write out the sums over 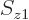 and
and 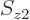 for
for 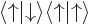 and verify that it is indeed the same as the written out sum for
and verify that it is indeed the same as the written out sum for 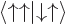 given in the answer for the previous question.
given in the answer for the previous question.
The underlying mathematical principle is that sums of products can be factored into separate sums as in:
This is similar to the observation in calculus that integrals of products can be factored into separate integrals:
Answer:
and written out
and multiplying out, and reordering the second and third factor in each term, you see it is the same as the expression obtained in the answer to the previous question,
![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![\begin{displaymath}
\sum_{{\rm all} S_{z1}} \sum_{{\rm all} S_{z2}} f(S_{z1}) ...
...S_{z1})\right] \left[\sum_{{\rm all} S_{z2}} g(S_{z2})\right]
\end{displaymath}](img539.gif)
![\begin{eqnarray*}\lefteqn{\int_{{\rm all} {\skew0\vec r}_1} \int_{{\rm all} {\...
...ec r}_2} g({\skew0\vec r}_2) { \rm d}^3 {\skew0\vec r}_2\right]
\end{eqnarray*}](img540.gif)
![\begin{displaymath}
\langle{\uparrow}\vert{\downarrow}\rangle\langle{\uparrow}\v...
...= \pm\frac 12\hbar}{\uparrow}(S_{z2}){\uparrow}(S_{z2})\right]
\end{displaymath}](img541.gif)