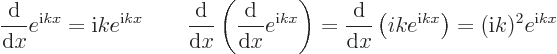| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.5.1 Solution eigvals-a
Question:
Show that 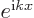 , above, is also an eigenfunction of
, above, is also an eigenfunction of 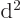
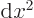 , but with eigenvalue
, but with eigenvalue 
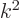 . In fact, it is easy to see that the square of any operator has the same eigenfunctions, but with the square eigenvalues.
. In fact, it is easy to see that the square of any operator has the same eigenfunctions, but with the square eigenvalues.
Answer:
Differentiate the exponential twice, [1, p. 60]:
So 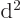
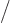
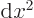 turns
turns 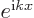 into
into 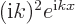 ; the eigenvalue is therefore
; the eigenvalue is therefore 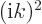 which equals
which equals 
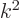 .
.
![]() ,
,![]()
![]()
![]() ,
,![]()
![]() .
.