| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.5.3 Solution eigvals-c
Question:
Show that 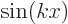 and
and 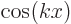 , with
, with 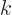 a constant, are eigenfunctions of the inversion operator
a constant, are eigenfunctions of the inversion operator 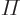 , which turns any function
, which turns any function 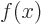 into
into 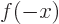 , and find the eigenvalues.
, and find the eigenvalues.
Answer:
By definition of 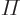 , and then using [1, p. 43]:
, and then using [1, p. 43]:
So by definition, both are eigenfunctions, and with eigenvalues  1 and 1, respectively.
1 and 1, respectively.
![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,
,