| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
4.1.4.1 Solution harmd-a
Question:
Write out the ground state wave function and show that it is indeed spherically symmetric.
Answer:
Repeating an earlier exercise, taking the generic expression
and substituting 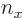

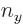

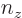
 0, you get the ground state eigenfunction
0, you get the ground state eigenfunction
Now substitute for 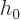 from table 4.1:
from table 4.1:
where the constant 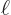 is as given in table 4.1. You can multiply out the exponentials:
is as given in table 4.1. You can multiply out the exponentials:
According to the Pythagorean theorem, 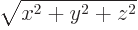 is the distance from the origin
is the distance from the origin 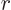 , so
, so
It follows that the wave function only depends on the distance 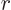 from the origin, not on the angular orientation compared to it. That is the definition of spherically symmetric: it looks the same from any angle.
from the origin, not on the angular orientation compared to it. That is the definition of spherically symmetric: it looks the same from any angle.
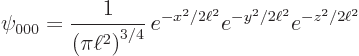
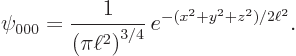
![]()
![]() ,
,