|
|
|
|
Next: 4.1.4.3 Solution harmd-c |
|
Question:
Show that the ground state wave function is maximal at the origin and, like all the other energy eigenfunctions, becomes zero at large distances from the origin.
Answer:
According to the answer to the previous question, the ground state is
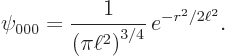
The other eigenfunctions do not necessarily have their maximum magnitude at the origin: for example, the shown states ![]()
![]()
For large negative values of its argument, an exponential becomes very small very quickly. So if the distance from the origin is large compared to ![]() ,
,
For example, if the distance from the origin is just 10 times ![]() ,
,
As far as the value of the other eigenfunctions at large distance from the origin is concerned, note from table 4.1 that all eigenfunctions take the generic form
It may be noted that the eigenfunctions do extend farther from the nominal position when the energy increases. The polynomials get nastier when the energy increases, but far enough away they must eventually always lose from the exponentials.