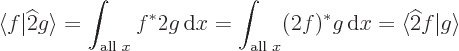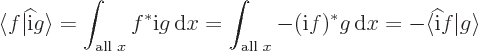| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.6.3 Solution herm-c
Question:
Show that the operator 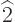 is a Hermitian operator, but
is a Hermitian operator, but 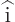 is not.
is not.
Answer:
By definition, 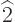 corresponds to multiplying by 2, so
corresponds to multiplying by 2, so 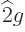 is simply the function
is simply the function 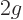 . Now write the inner product
. Now write the inner product 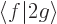 and see whether it is the same as
and see whether it is the same as 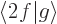 for any
for any 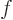 and
and 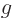 :
:
since the complex conjugate does not affect a real number like 2. So 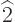 is indeed Hermitian.
is indeed Hermitian.
On the other hand,
so 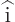 is not Hermitian. An operator like
is not Hermitian. An operator like 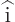 that flips over the sign of an inner product if it is moved to the other side is called
that flips over the sign of an inner product if it is moved to the other side is called skew-Hermitian
. An operator like 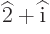 is neither Hermitian nor skew-Hermitian.
is neither Hermitian nor skew-Hermitian.
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() :
: