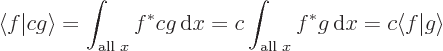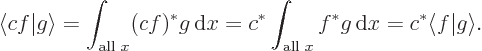| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
2.6.4 Solution herm-d
Question:
Generalize the previous question, by showing that any complex constant 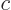 comes out of the right hand side of an inner product unchanged, but out of the left hand side as its complex conjugate;
comes out of the right hand side of an inner product unchanged, but out of the left hand side as its complex conjugate;
As a result, a number 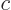 is only a Hermitian operator if it is real: if
is only a Hermitian operator if it is real: if 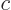 is complex, the two expressions above are not the same.
is complex, the two expressions above are not the same.
Answer:
Since constants can be taken out of an integral:
![]()