5.2.1.1 So­lu­tion hmola-a

Ques­tion:

Ver­ify that the re­pul­sive po­ten­tial be­tween the elec­trons is in­fi­nitely large when the elec­trons are at the same po­si­tion.

Note: You might there­fore think that the wave func­tion needs to be zero at the lo­ca­tions in six-di­men­sion­al space where 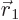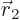${\skew0\vec r}_1$ $\vphantom0\raisebox{1.5pt}{$=$}$ ${\skew0\vec r}_2$. Some au­thors re­fer to that as a Coulomb hole.” But the truth is that in quan­tum me­chan­ics, elec­trons are smeared out due to un­cer­tainty. That causes elec­tron 1 to “see elec­tron 2 at all sides, and vice-versa, and they do there­fore not en­counter any un­usu­ally large po­ten­tial when the wave func­tion is nonzero at 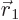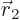${\skew0\vec r}_1$ $\vphantom0\raisebox{1.5pt}{$=$}$ ${\skew0\vec r}_2$. In gen­eral, it is just not worth the trou­ble for the elec­trons to stay away from the same po­si­tion: that would re­duce their un­cer­tainty in po­si­tion, in­creas­ing their un­cer­tainty-de­manded ki­netic en­ergy.

An­swer:

The re­pul­sive po­ten­tial is the term

$$\frac{e^2}{4\pi\epsilon_0} \frac 1{\vert{\skew0\vec r}_1 - {\skew0\vec r}_2\vert}$$

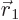
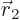and when ${\skew0\vec r}_1$ $\vphantom0\raisebox{1.5pt}{$=$}$ ${\skew0\vec r}_2$, you are di­vid­ing by zero.