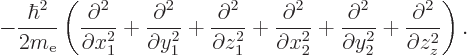| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
5.2.1.2 Solution hmola-b
Question:
Note that the total kinetic energy term is simply a multiple of the six-dimensional Laplacian operator. It treats all Cartesian position coordinates exactly the same, regardless of which direction or which electron it is. Is this still the case if other particles are involved?
Answer:
The kinetic energy of the two electrons is
and the terms within the parentheses are the six-dimensional Laplacian. But if other particles would be involved, they would have a different value of 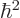
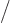
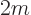 and the total operator would no longer be the normal Laplacian.
and the total operator would no longer be the normal Laplacian.
All else being the same, heavier particles would have less kinetic energy. But, of course, all else is usually not the same. For example, the atoms in noble gases have the same kinetic energy at the same temperature regardless of atom mass.