| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
5.2.4.1 Solution hmold-a
Question:
Obviously, the visual difference between the various states is minor. It may even seem counter-intuitive that there is any difference at all: the states 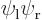 and
and 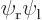 are exactly the same physically, with one electron around each proton. So why would their combinations be any different?
are exactly the same physically, with one electron around each proton. So why would their combinations be any different?
The quantum difference would be much more clear if you could see the full six-dimensional wave function, but visualizing six-dimensional space just does not work. However, if you restrict yourself to only looking on the  -axis through the nuclei, you get a drawable
-axis through the nuclei, you get a drawable 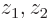 -plane describing near what axial combinations of positions you are most likely to find the two electrons. In other words: what would be the chances of finding electron 1 near some axial position
-plane describing near what axial combinations of positions you are most likely to find the two electrons. In other words: what would be the chances of finding electron 1 near some axial position 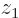 and electron 2 at the same time near some other axial position
and electron 2 at the same time near some other axial position 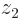 ?
?
Try to guess these probabilities in the 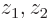 -plane as grey tones, (darker if more likely), and then compare with the answer.
-plane as grey tones, (darker if more likely), and then compare with the answer.
Answer:
Here are the pictures, assuming the origin is halfway in between the protons:
Figure 5.1:
Wave functions on the  -axis through the nuclei. From left to right:
-axis through the nuclei. From left to right: 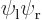 ,
, 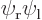 , the symmetric combination
, the symmetric combination 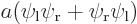 , and the antisymmetric one
, and the antisymmetric one 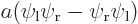 .
.
![\begin{figure}\centering {}
\setlength{\unitlength}{1pt}
\begin{picture}(422,97...
... \multiput(-163,92)(108,0){4}{\makebox(0,0)[r]{$z_2$}}
\end{picture}\end{figure}](img474.gif) |
These results can be explained as follows: For the state 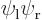 , electron 1 is around the left proton, so its likely
, electron 1 is around the left proton, so its likely  positions are clustered around the position
positions are clustered around the position 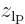 of that proton, indicated by a tick mark on the negative
of that proton, indicated by a tick mark on the negative 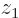 -axis in figure 5.1. Similarly electron 2 is around the right proton, so its
-axis in figure 5.1. Similarly electron 2 is around the right proton, so its 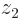 positions are clustered around the positive value
positions are clustered around the positive value 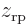 indicated by the tick mark on the positive
indicated by the tick mark on the positive 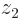 axis. This means the wave function,
axis. This means the wave function, 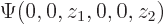 , will look as shown in the left picture of figure 5.1. It will be mostly in the quadrant of negative
, will look as shown in the left picture of figure 5.1. It will be mostly in the quadrant of negative 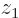 and positive
and positive 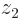 .
.
Similarly 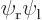 will look as the second picture. Here the positions of electron 1 cluster around the positive position of the right proton and those of electron 2 around the negative position of the left proton.
will look as the second picture. Here the positions of electron 1 cluster around the positive position of the right proton and those of electron 2 around the negative position of the left proton.
When you average the two states symmetrically, you get a two-blob picture like the third picture. Now it is electron 1 around the left proton and electron 2 around the right one or vice-versa. But there is still almost no probability of finding both protons in the first quadrant, both near the right proton. Nor are you likely to find them in the third quadrant, both near the left proton.
If you average the first two states antisymmetrically, you get the fourth picture. In the antisymmetric combination, the wave function is zero on the symmetry line between the blobs.
You see that the states are really different when looked at in the full six-dimensional space.
![]()
![]()
![]() -
-![]() -
-![]()
![]() ?
?![]() -
-![\begin{figure}\centering {}
\setlength{\unitlength}{1pt}
\begin{picture}(422,97...
... \multiput(-163,92)(108,0){4}{\makebox(0,0)[r]{$z_2$}}
\end{picture}\end{figure}](img474.gif)
![]() ,
,![]()
![]()
![]() -
-![]()
![]()
![]()
![]() ,
,![]()
![]() .
.![]()