| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
5.2.4.2 Solution hmold-b
Question:
Based on the previous question, how would you think the probability density 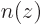 would look on the axis through the nuclei, again ignoring the existence of positions beyond the axis?
would look on the axis through the nuclei, again ignoring the existence of positions beyond the axis?
Answer:
For any state, the probability of finding electron 1 near a given  , regardless of where electron 2 is, is found by setting
, regardless of where electron 2 is, is found by setting 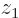 equal to
equal to  and integrating over all possible positions
and integrating over all possible positions 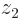 for electron 2. For the two-dimensional state
for electron 2. For the two-dimensional state 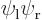 shown in the left column of figure 5.2, you are then integrating over vertical lines in the top picture; imagine moving all blank ink vertically towards the
shown in the left column of figure 5.2, you are then integrating over vertical lines in the top picture; imagine moving all blank ink vertically towards the 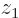 axis and then setting
axis and then setting 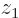

 . The resulting curve is shown immediately below. As expected, electron 1 is in this state most likely to be found somewhere around
. The resulting curve is shown immediately below. As expected, electron 1 is in this state most likely to be found somewhere around 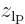 , the negative position of the left proton. Regardless of where electron 2 is.
, the negative position of the left proton. Regardless of where electron 2 is.
Figure 5.2:
Probability density functions on the  -axis through the nuclei. From left to right:
-axis through the nuclei. From left to right: 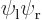 ,
, 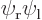 , the symmetric combination
, the symmetric combination 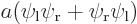 , and the antisymmetric one
, and the antisymmetric one 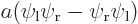 . From top to bottom, the top row of curves show the probability of finding electron 1 near
. From top to bottom, the top row of curves show the probability of finding electron 1 near  regardless where electron 2 is. The second row shows the probability of finding electron 2 near
regardless where electron 2 is. The second row shows the probability of finding electron 2 near  regardless where electron 1 is. The third row shows the total probability of finding either electron near
regardless where electron 1 is. The third row shows the total probability of finding either electron near  , the sum of the previous two rows. The fourth row shows the same as the third, but assuming the true three-dimensional world rather than just the line through the nuclei.
, the sum of the previous two rows. The fourth row shows the same as the third, but assuming the true three-dimensional world rather than just the line through the nuclei.
![\begin{figure}\centering {}
\setlength{\unitlength}{1pt}
\begin{picture}(422,24...
...}} \multiput(-164,35)(108,0){4}{\makebox(0,0)[r]{$n$}}
\end{picture}\end{figure}](img479.gif) |
(Note that all possible positions of electron 2 should really be found by integrating over all possible positions in three dimensions, not just axial ones. The final row in the figure gives the total probabilities when corrected for that. But the idea is the same, just harder to visualize.)
The probability density at a given value of  also needs to include the possibility of finding electron 2 there. That probability is found by setting
also needs to include the possibility of finding electron 2 there. That probability is found by setting 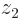

 and then integrating over all possible values of
and then integrating over all possible values of 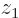 . You are now moving the blank ink horizontally towards the
. You are now moving the blank ink horizontally towards the 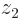 axis, and then setting
axis, and then setting 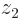

 . The resulting curve is shown in the second graph in the left column of figure 5.2. As expected, electron 2 is most likely to be found somewhere around
. The resulting curve is shown in the second graph in the left column of figure 5.2. As expected, electron 2 is most likely to be found somewhere around 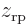 , the positive position of the right proton.
, the positive position of the right proton.
To get the probability density, the chance of finding either proton near  , you need to add the two curves together. That is done in the third graph in the left column of figure 5.2. An electron is likely to be somewhere around each proton. This graph looks exactly like the correct three-dimensional curve shown in the bottom graph, but that is really just a coincidence.
, you need to add the two curves together. That is done in the third graph in the left column of figure 5.2. An electron is likely to be somewhere around each proton. This graph looks exactly like the correct three-dimensional curve shown in the bottom graph, but that is really just a coincidence.
The states 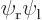 and
and 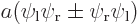 can be integrated similarly; they are shown in the subsequent columns in figure 5.2. Note how the line of zero wave function in the antisymmetric case disappears during the integrations. Also note that really, the probability density functions of the symmetric and antisymmetric states are quite different, though they look qualitatively the same.
can be integrated similarly; they are shown in the subsequent columns in figure 5.2. Note how the line of zero wave function in the antisymmetric case disappears during the integrations. Also note that really, the probability density functions of the symmetric and antisymmetric states are quite different, though they look qualitatively the same.
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() ,
,![\begin{figure}\centering {}
\setlength{\unitlength}{1pt}
\begin{picture}(422,24...
...}} \multiput(-164,35)(108,0){4}{\makebox(0,0)[r]{$n$}}
\end{picture}\end{figure}](img479.gif)
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]() .
.![]() ,
,![]() ,
,![]()
![]()