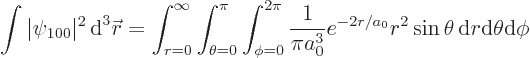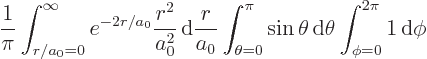|
|
|
|
Next: 4.3.2.2 Solution hydb-b |
|
Question:
Use the tables for the radial wave functions and the spherical harmonics to write down the wave function
Check that the state is normalized. Note: ![]()
![]()
![]() .
.
Answer:
The tables show that ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
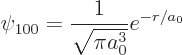
The total probability of finding the particle integrated over all possible positions is, using the techniques of volume integration in spherical coordinates: