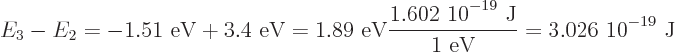4.3.3.3 So­lu­tion hydc-c

Ques­tion:

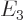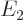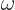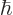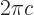
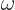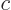Based on the re­sults of the pre­vi­ous ques­tion, what is the color of the light emit­ted in a Balmer tran­si­tion from en­ergy $E_3$ to $E_2$? The Planck-Ein­stein re­la­tion says that the an­gu­lar fre­quency $\omega$ of the emit­ted pho­ton is its en­ergy di­vided by $\hbar$, and the wave length of light is $2{\pi}c$$\raisebox{.5pt}{$/$}$​$\omega$ where $c$ is the speed of light. Typ­i­cal wave lengths of vis­i­ble light are: vi­o­let 400 nm, in­digo 445 nm, blue 475 nm, green 510 nm, yel­low 570 nm, or­ange 590 nm, red 650 nm.

An­swer:

The en­ergy car­ried away by the pho­ton is the en­ergy lost by the elec­tron, which is

$$E_3-E_2 = -\mbox{1.51 eV}+\mbox{3.4 eV}= \mbox{1.89 eV} \fra... ...OW9,{-19}$ J}}{\mbox{1 eV}} = \mbox{3.026 10$\POW9,{-19}$ J}$$

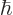
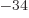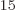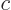
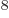Di­vid­ing by $\hbar$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1.054 10$\POW9,{-34}$ J s gives the an­gu­lar fre­quency to be 2.87 10$\POW9,{15}$/s, and then the wave length is 656 nm, us­ing $c$ $\vphantom0\raisebox{1.5pt}{$=$}$ 3 10$\POW9,{8}$ m/s. That will be red light.