| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
5.8.1 Solution matfor-a
Question:
As a relatively simple example, work out the above ideas for the 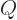
 2 hydrogen molecule spatial states
2 hydrogen molecule spatial states 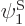

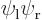 and
and 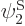

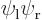 . Write the matrix eigenvalue problem and identify the two eigenvalues and eigenvectors. Compare with the results of section 5.3.
. Write the matrix eigenvalue problem and identify the two eigenvalues and eigenvectors. Compare with the results of section 5.3.
Assume that 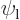 and
and 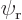 have been slightly adjusted to be orthonormal. Then so are
have been slightly adjusted to be orthonormal. Then so are 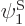 and
and 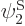 orthonormal, since the various six-dimensional inner product integrals, like
orthonormal, since the various six-dimensional inner product integrals, like
can according to the rules of calculus be factored into three-dimensional integrals as
which is zero if 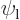 and
and 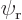 are orthonormal.
are orthonormal.
Also, do not try to find actual values for 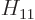 ,
, 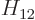 ,
, 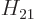 , and
, and 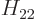 . As section 5.2 noted, that can only be done numerically. Instead just refer to
. As section 5.2 noted, that can only be done numerically. Instead just refer to 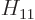 as
as 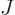 and to
and to 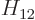 as
as 
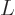 :
:
Next note that you also have
because they are the exact same inner product integrals; the difference is just which electron you number 1 and which one you number 2 that determines whether the wave functions are listed as 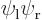 or
or 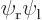 .
.
Answer:
Using the abbreviations 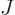 and
and 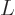 , the matrix eigenvalue problem becomes
, the matrix eigenvalue problem becomes
or taking everything to the left hand side,
For this homogeneous system of equations to have a solution other than the trivial one 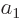

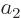
 0, the determinant of the matrix must be zero:
0, the determinant of the matrix must be zero:
which allows for the two possibilities
So there are two energy eigenvalues:
In the first case, since according to the equations above
it follows that 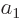 and
and 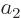 must be equal, producing the eigenfunction
must be equal, producing the eigenfunction
and normalization shows that 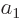
 1/
1/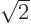 , assuming you take it real and positive, (and assuming that
, assuming you take it real and positive, (and assuming that 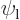 and
and 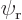 are really adjusted to be orthonormal as assumed in this particular question).
are really adjusted to be orthonormal as assumed in this particular question).
So the first energy eigenstate is
Similarly the second energy eigenstate is
Comparing with section 5.3, the first eigenstate can be recognized as the ground state in which the nuclei share the electrons symmetrically. The second eigenstate is the excited-energy antisymmetric state in which the electrons share the electrons antisymmetrically. Other states of this type, like simply 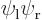 , say, have expectation energy somewhere in between
, say, have expectation energy somewhere in between 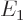 and
and 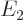 , but they are not eigenstates and do not have definite energy.
, but they are not eigenstates and do not have definite energy.
Of course, the analysis here is approximate. But as discussed more in the earlier section 5.2, the true ground state is really symmetric, and the excited energy eigenstate really is antisymmetric. After all, the Hamiltonian commutes with the operation of swapping the electrons, (swapping the electrons does not do anything physically,) so the energy eigenstates must also be eigenstates of the swapping operator. The symmetric state is an eigenstate of the swapping operator with eigenvalue 1, it stays the same, and the antisymmetric state is an eigenstate with eigenvalue  1; it changes sign under the swap.
1; it changes sign under the swap.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
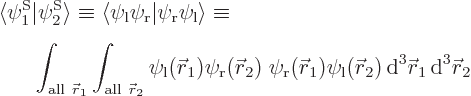
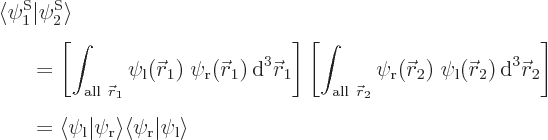
![]() ,
,![]() ,
,![]() ,
,![]() .
.![]()
![]()
![]()
![]()
![]() :
: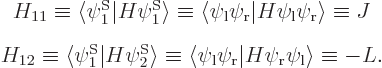
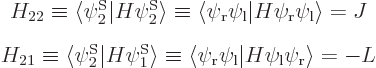
![]()
![]() ,
,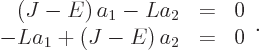
![]()
![]()
![]()
![]()
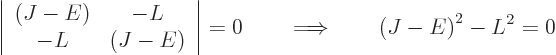
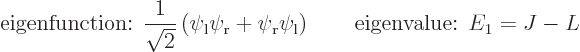
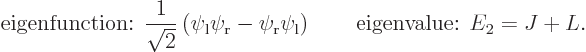
![]() ,
,![]()
![]() ,
,![]() 1
1