|
|
|
|
Next: 5.9 Heavier Atoms |
|
Question:
Find the eigenstates for the same problem, but now including spin.
As section 5.7 showed, the antisymmetric wave function with spin consists of a sum of six Slater determinants. Ignoring the highly excited first and sixth determinants that have the electrons around the same nucleus, the remaining ![]()
![]()
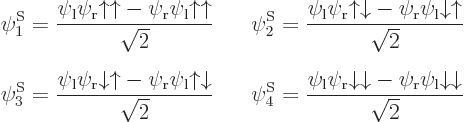
Note that the Hamiltonian does not involve spin, to the approximation used in most of this book, so that, following the techniques of section 5.5, an inner product like ![]()
![]()
![]()
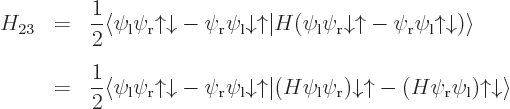
If you do not have experience with linear algebra, you may want to skip this question, or better, just read the solution. However, the four eigenvectors are not that hard to guess; maybe easier to guess than correctly derive.
Answer:
Evaluating all 16 inner products ![]()
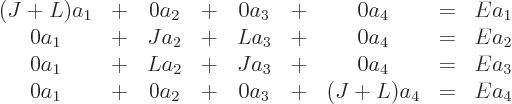
After bringing everything to the left hand side, the determinant of the resulting matrix can again be set to zero, and the possible energy values found. From those the eigenvectors can be deduced. It turns out that the larger eigenvalue is triply degenerate, so the three corresponding eigenvectors are not unique; more than one acceptable choice exists for them. However, you do have to normalize them to unit length and ensure that they are mutually orthogonal.
Rather than going through that math, it is quicker just to guess the eigenvectors. One guess that works is
A similar guess that works is
The final eigenvector