| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
7.1.2.1 Solution schrodsol-a
Question:
The energy of a photon is 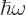 where
where 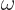 is the classical frequency of the electromagnetic field produced by the photon. So what is
is the classical frequency of the electromagnetic field produced by the photon. So what is 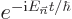 for a photon? Are you surprised by the result?
for a photon? Are you surprised by the result?
Answer:
The exponential 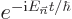 becomes
becomes 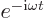 . That is the classical time dependence of the electromagnetic field.
. That is the classical time dependence of the electromagnetic field.
The result is not really surprising, because of the wave-particle dualism of quantum mechanics. Classical physics understands the wave nature of light well, and not its particle nature. This is the opposite of the situation for an electron, where classical physics understands the particle nature, and not the wave nature.
![]()
![]()
![]()
![]()
![]() .
.