| Quantum Mechanics Solution Manual |
|
© Leon van Dommelen |
|
7.1.2.2 Solution schrodsol-b
Question:
For the one-dimensional harmonic oscillator, the energy eigenvalues are
Write out the coefficients 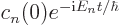 for those energies.
for those energies.
Now classically, the harmonic oscillator has a natural frequency 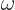 . That means that whenever
. That means that whenever 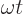 is a whole multiple of
is a whole multiple of 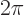 , the harmonic oscillator is again in the same state as it started out with. Show that the coefficients of the energy eigenfunctions have a natural frequency of
, the harmonic oscillator is again in the same state as it started out with. Show that the coefficients of the energy eigenfunctions have a natural frequency of 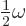 ;
; 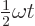 must be a whole multiple of
must be a whole multiple of 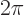 for the coefficients to return to their original values.
for the coefficients to return to their original values.
Answer:
The coefficients are
Now if 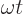 is
is 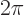 , the argument of the exponential equals
, the argument of the exponential equals 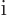 times an odd multiple of
times an odd multiple of 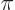 . That makes the exponential equal to minus one. It takes until
. That makes the exponential equal to minus one. It takes until 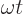

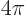 until the exponential returns to its original value one.
until the exponential returns to its original value one.
![]() .
.![]()
![]() ,
,![]() ;
;![]()
![]()