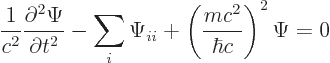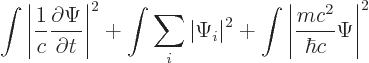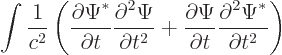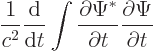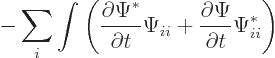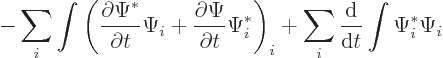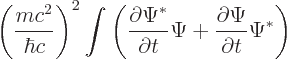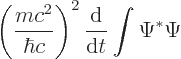| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.32 Integral conservation laws
This section derives the integral conservation laws given in
addendum {A.14}.
The rules of engagement are as follows:
- The Cartesian axes are numbered using an index
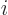 , with
, with
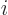
 1, 2, and 3 for
1, 2, and 3 for  ,
, 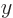 , and
, and 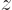 respectively.
respectively.
- Also,
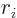 indicates the coordinate in the
indicates the coordinate in the 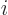 direction,
direction,
 ,
, 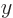 , or
, or 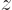 .
.
- Derivatives with respect to a coordinate
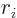 are indicated by
a simple subscript
are indicated by
a simple subscript 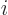 .
.
- Time derivatives are indicated by a subscript t.
- A bare
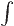 integral sign is assumed to be an integration over
all space, or over the entire box for particles in a box. The
integral sign is assumed to be an integration over
all space, or over the entire box for particles in a box. The
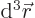 is normally omitted for brevity and to be understood.
is normally omitted for brevity and to be understood.
- A superscript
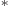 indicates a complex conjugate.
indicates a complex conjugate.
First it will be shown that according to the Schrödinger equation
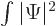 is constant. The Schrödinger equation in free space is
is constant. The Schrödinger equation in free space is
Taking the right hand term to the other side and writing it in index
notation gives
Multiply the left hand side by 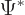

 and add the complex
conjugate of the same equation to get
and add the complex
conjugate of the same equation to get
To show that the integral 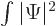 is constant, it must be shown
that its time derivative is zero. Now the first two terms above are
the time derivative of
is constant, it must be shown
that its time derivative is zero. Now the first two terms above are
the time derivative of 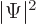

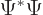 . So
integrated over all space, they give the time derivative that must be
shown to be zero. And the equation above shows that it is indeed zero
provided that the remaining sum in it integrates to zero over all
space.
. So
integrated over all space, they give the time derivative that must be
shown to be zero. And the equation above shows that it is indeed zero
provided that the remaining sum in it integrates to zero over all
space.
The constant is not important in showing that this is true, so just
examine for any 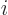
This equals
as can be seen by differentiating out the parenthetical expression
with respect to 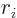 . The above integrand can be integrated
with respect to
. The above integrand can be integrated
with respect to 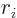 . It will then be zero for a periodic box
since the expression in parenthesis is the same at the upper and lower
limits of integration. It will also be zero for an impenetrable
container, since
. It will then be zero for a periodic box
since the expression in parenthesis is the same at the upper and lower
limits of integration. It will also be zero for an impenetrable
container, since 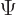 will then be zero on the surface of the
container. It will also be zero in an infinite region provided that
will then be zero on the surface of the
container. It will also be zero in an infinite region provided that
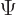 and its derivatives vanish at large distances.
and its derivatives vanish at large distances.
There is another way to see that 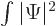 is constant. First recall
that any solution of the Schrödinger equation takes the form
is constant. First recall
that any solution of the Schrödinger equation takes the form
Here the 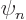 are the energy eigenfunctions. Then
are the energy eigenfunctions. Then
Now because of orthonormality of the eigenfunctions, the integration
only produces a nonzero result when 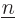

 , and then
the product of the eigenfunctions integrates to 1. So
, and then
the product of the eigenfunctions integrates to 1. So
That does not depend on time, and the normalization requirement makes
it 1.
This also clarifies what goes wrong with the Klein-Gordon equation.
For the Klein-Gordon equation
The first sum are the particle states and the second sum the
antiparticle states. That gives:
The final two terms in the sum oscillate in time. So the integral is
no longer constant.
The exception is if there are only particle states (no 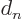 ) or only
antiparticle states (no
) or only
antiparticle states (no 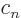 ). In those two cases, the integral is
constant. In general
). In those two cases, the integral is
constant. In general
where the integrated square magnitudes of 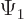 and
and 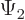 are
constant.
are
constant.
Next it will be shown that the rearranged Klein-Gordon equation
preserves the sum of integrals
To do so it suffices to show that the sum of the time derivatives of
the three integrals is zero. That can be done by multiplying the
Klein-Gordon equation by 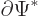

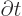 , adding
the complex conjugate of the obtained equation, and integrating over
all space. Each of the three terms in the Klein-Gordon equation will
then give one of the three needed time derivatives. So their sum will
indeed be zero.
, adding
the complex conjugate of the obtained equation, and integrating over
all space. Each of the three terms in the Klein-Gordon equation will
then give one of the three needed time derivatives. So their sum will
indeed be zero.
To check that, look at what each term in the Klein-Gordon equation
produces separately. The first term gives
or taking one time derivative outside the integral, that is
That is the first needed time derivative, since a number times its
complex conjugate is the square magnitude of that number.
The second term in the Klein-Gordon equation produces
That equals
as can be seen by differentiating out the parenthetical expression in
the first integral with respect to 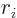 and bringing the time
derivative in the second term inside the integral. The first integral
above is zero for a periodic box, for an impenetrable container, and
for infinite space for the same reasons as given in the derivation for
the Schrödinger equation. The second term above is the needed
second time derivative.
and bringing the time
derivative in the second term inside the integral. The first integral
above is zero for a periodic box, for an impenetrable container, and
for infinite space for the same reasons as given in the derivation for
the Schrödinger equation. The second term above is the needed
second time derivative.
The final of the three terms in the Klein-Gordon equation produces
That equals
as can be seen by bringing the time derivative inside the integral.
This is the last of the three needed time derivatives.
![]()
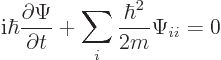
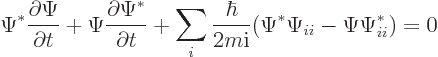
![]()
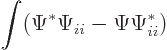
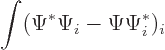
![]()
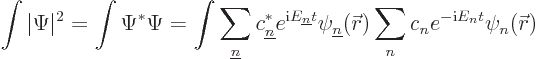
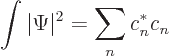
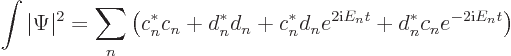
![]() )
)![]() )
)