| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.14 The Klein-Gordon equation
The Schrödinger equation for the quantum wave function is based on
the nonrelativistic expression for the energy of a particle. This
addendum looks at the simplest relativistic equation for wave
functions, called the Klein-Gordon equation. The discussion will
largely be restricted to a spinless particle in empty space, where
there is no potential energy. However, the Klein-Gordon equation is
the first step to more complex relativistic equations.
Recall first how the Schrödinger equation arose. If there is no potential
energy, classical physics says that the energy  is just the kinetic
energy
is just the kinetic
energy 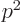

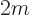 of the particle. Here
of the particle. Here 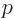 is the linear momentum of
the particle and
is the linear momentum of
the particle and 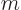 its mass. Quantum mechanics replaces the energy
its mass. Quantum mechanics replaces the energy
 by the operator
by the operator 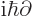

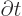 and the momentum
and the momentum
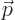 by
by 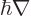

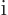 , where
, where
Then it applies the resulting operators on the wave function
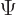 . That then produces the Schrödinger equation
. That then produces the Schrödinger equation
Solutions with a definite value  for the energy take the form
for the energy take the form
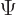

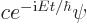 . Substituting that into
the Schrödinger equation and rearranging produces the so-called Hamiltonian
eigenvalue problem
. Substituting that into
the Schrödinger equation and rearranging produces the so-called Hamiltonian
eigenvalue problem
Here 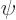 is called the energy eigenfunction.
is called the energy eigenfunction.
According to classical relativity however, the energy  of a
particle in empty space is not just kinetic energy, but also rest mass
energy
of a
particle in empty space is not just kinetic energy, but also rest mass
energy 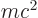 , where
, where 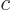 is the speed of light. In particular,
chapter 1.1.2 (1.2),
is the speed of light. In particular,
chapter 1.1.2 (1.2),
The momentum can be identified with the same operator as before. But
square roots of operators are very ugly. So the smart thing to do is
to square both sides above. Making the same substitutions as for the
Schrödinger equation and cleaning up then gives the “Klein-Gordon equation”
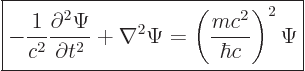 |
(A.43) |
Solutions 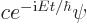 with definite energy
with definite energy  satisfy
the
satisfy
the time-independent Klein-Gordon equation
or square Hamiltonian eigenvalue problem
This may be rewritten in a form so that both the Schrödinger equation
and the Klein-Gordon equation are covered:
 |
(A.44) |
Here the constant 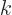 is called the
is called the wave number.
Note that the nonrelativistic energy does not include the rest mass
energy. When that is taken into account, the Schrödinger expression
for 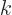 above is the nonrelativistic approximation for the
Klein-Gordon
above is the nonrelativistic approximation for the
Klein-Gordon 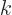 as it should be.
as it should be.
Further note that relativistic or not, the magnitude of linear
momentum 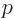 is given by the “de Broglie relation”
is given by the “de Broglie relation” 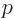

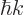 . That is
because relativistic or not the momentum operator is
. That is
because relativistic or not the momentum operator is
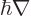

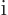 , so
, so 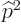


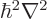 .
Similarly, relativistic or not, the energy is associated the operator
.
Similarly, relativistic or not, the energy is associated the operator
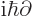

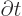 . That means that the
time-dependent factor in states of definite energy is
. That means that the
time-dependent factor in states of definite energy is
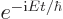 . That allows the energy to be associated
with an
. That allows the energy to be associated
with an angular frequency
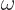 by writing the
exponential as
by writing the
exponential as 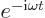 . The relationship between
energy and frequency is then
. The relationship between
energy and frequency is then 

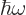 . That is
known as the “Planck-Einstein relation” when applied to photons. In short,
relativistic or not,
. That is
known as the “Planck-Einstein relation” when applied to photons. In short,
relativistic or not,
 |
(A.45) |
The wave number 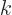 is the quantum number of linear momentum, and the
angular frequency
is the quantum number of linear momentum, and the
angular frequency 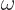 is the one of energy. See addendum
{A.19} for more on how these numbers arise
physically from symmetries of nature.
is the one of energy. See addendum
{A.19} for more on how these numbers arise
physically from symmetries of nature.
It may be noted that Schrödinger wrote down the Klein-Gordon
equation first. But when he added the Coulomb potential, he was not
able to get the energy levels of the hydrogen atom. To fix that
problem, he wrote down the simpler nonrelativistic equation that bears
his name. The problem in the relativistic case is that after you add
the Coulomb potential to the energy, you can no longer square away the
square root. Eventually, Dirac figured out how to get around that
problem, chapter 12.12 and {D.81}. In brief,
he assumed that the wave function for the electron is not a scalar,
but a four-dimensional vector, (two spin states for the electron, plus
two spin states for the associated antielectron, or positron.) Then he
assumed that the square root takes a simple form for that vector.
Since this addendum assumes a particle in empty space, the problem with
the Coulomb potential does not arise. But there are other issues.
The good news is that according to the Klein-Gordon equation, effects
do not propagate at speeds faster than the speed of light. That is
known from the theory of partial differential equations. In classical
physics, effects cannot propagate faster than the speed of light, so
it is somewhat reassuring that the Klein-Gordon equation respects
that.
Also, all inertial observers agree about the Klein-Gordon equation,
regardless of the motion of the observer. That is because all
inertial observers agree about the rest mass 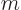 of a particle and the
value of the speed of light
of a particle and the
value of the speed of light 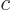 . So they all agree about the
right hand side in the Klein-Gordon equation (A.43). And the
left hand side in the Klein-Gordon equation is also the same for all
inertial observers. You can crunch that out using the Lorentz
transform as given in chapter 1.2.1 (1.6).
(Those familiar with index notation as briefly described in chapter
1.2.5 recognize the entire left hand side as being simply
. So they all agree about the
right hand side in the Klein-Gordon equation (A.43). And the
left hand side in the Klein-Gordon equation is also the same for all
inertial observers. You can crunch that out using the Lorentz
transform as given in chapter 1.2.1 (1.6).
(Those familiar with index notation as briefly described in chapter
1.2.5 recognize the entire left hand side as being simply
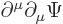 . That is unchanged going from
one observer to the next, because the upper index transforms under the
Lorentz transform and the lower index under the inverse Lorentz
transform. The operator
. That is unchanged going from
one observer to the next, because the upper index transforms under the
Lorentz transform and the lower index under the inverse Lorentz
transform. The operator 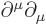 is called the
“D’Alembertian,” much like
is called the
“D’Alembertian,” much like  is called the
Laplacian.)
is called the
Laplacian.)
But the bad news is that the Klein-Gordon equation does not
necessarily preserve the integral of the square magnitude of the wave
function. The Schrödinger equation implies that,
{D.32},
The wave function is then normalized so that the constant is 1.
According to the Born statistical interpretation, chapter
3.1, the integral above represents the probability of
finding the particle if you look at all possible positions. That must
be 1 at whatever time you look; the particle must be somewhere.
Because the Schrödinger equation ensures that the integral above
stays 1, it ensures that the particle cannot just disappear, and that
no second particle can show up out of nowhere.
But the Klein-Gordon equation does not preserve the integral above.
Therefore the number of particles is not necessarily preserved. That
is not as bad as it looks, anyway, because in relativity the
mass-energy equivalence allows particles to be created or destroyed,
chapter 1.1.2. But certainly, the interpretation of the
wave function is not a priori obvious. The integral that the
Klein-Gordon equation does preserve is, {D.32},
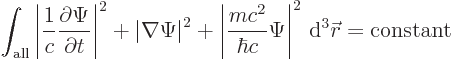
It is maybe somewhat comforting that according to this expression, the
integral of 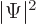 must at least remain bounded. That does assume
that the rest mass
must at least remain bounded. That does assume
that the rest mass 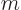 of the particle is not zero. Photons need not
apply.
of the particle is not zero. Photons need not
apply.
Another problem arises because even though the square energy 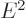 is
normally positive, the energy
is
normally positive, the energy  itself can still be both positive or
negative. That is a problem, because then there is no lower limit to
the energy, there is no ground state. The particle can then
transition to states of lower and lower energy tending to minus
infinity. That would release unbounded amounts of energy. (Since the
kinetic energy can be arbitrarily large, the positive value of the
energy can be arbitrarily large. That makes the negative value of the
energy also arbitrarily large in magnitude.)
itself can still be both positive or
negative. That is a problem, because then there is no lower limit to
the energy, there is no ground state. The particle can then
transition to states of lower and lower energy tending to minus
infinity. That would release unbounded amounts of energy. (Since the
kinetic energy can be arbitrarily large, the positive value of the
energy can be arbitrarily large. That makes the negative value of the
energy also arbitrarily large in magnitude.)
You might say, just ignore the negative energy possibility. But Dirac
found that that does not work; you need both positive and negative
energy states to explain such things as the hydrogen energy levels.
The way Dirac solved the problem for electrons is to assume that all
negative states are already filled with electrons. Unfortunately,
that does not work for bosons, since any number of bosons can go into
a state.
The modern view is to consider the negative energy solutions to
represent antiparticles. In that view, antiparticles have positive
energy, but move backwards in time. For example, Dirac’s negative
energy states are not electrons with negative energy, but positrons
with positive energy. Positrons are then electrons that move backward
in time. To illustrate the idea, consider two hypothetical wave
functions of the form
where  is the positive root for the energy. The first wave
function is no problem; it is of the form of a wave function that you
would get for a nonrelativistic particle of energy
is the positive root for the energy. The first wave
function is no problem; it is of the form of a wave function that you
would get for a nonrelativistic particle of energy  . The
second wave function is the problem. It is not considered to be a
particle of negative energy
. The
second wave function is the problem. It is not considered to be a
particle of negative energy 
 . Instead it is considered an
antiparticle of positive energy
. Instead it is considered an
antiparticle of positive energy  that moves backward in time. It
is the reversal of the relevant direction of time that causes the sign
change in the argument of the exponential.
that moves backward in time. It
is the reversal of the relevant direction of time that causes the sign
change in the argument of the exponential.
You see why so much quantum physics is done using nonrelativistic
equations.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,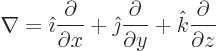
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]() .
.![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]() .
.![]() .
.![]()
![]()
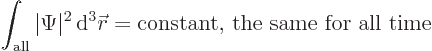
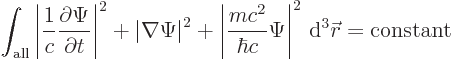
![]()
![]()