| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.13 Integral Schrödinger equation
The Hamiltonian eigenvalue problem, or time-independent Schrödinger
equation, is the central equation of quantum mechanics. It reads
Here 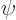 is the wave function,
is the wave function, 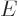 is the energy of the state
described by the wave function,
is the energy of the state
described by the wave function, 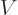 is the potential energy,
is the potential energy, 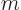 is
the mass of the particle, and
is
the mass of the particle, and 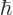 is the scaled Planck constant.
is the scaled Planck constant.
The equation also involves the Laplacian operator, defined as
Therefore the Hamiltonian eigenvalue problem involves partial
derivatives, and it is called a partial differential equation.
However, it is possible to manipulate the equation so that the wave
function 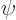 appears inside an integral rather than inside partial
derivatives. The equation that you get this way is called the
appears inside an integral rather than inside partial
derivatives. The equation that you get this way is called the
integral Schrödinger equation.
It takes the form,
{D.31}:
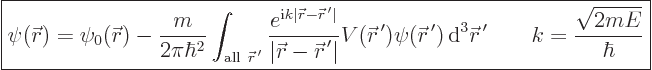 |
(A.42) |
Here 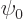 is any wave function of energy
is any wave function of energy 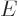 in free space. In
other words
in free space. In
other words 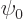 is any wave function for the particle in the
absence of the potential
is any wave function for the particle in the
absence of the potential 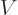 . The constant
. The constant 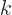 is a measure of
the energy of the particle. It also corresponds to a wave number far
from the potential. While not strictly required, the integral Schrödinger
equation above tends to be most suited for particles in infinite
space.
is a measure of
the energy of the particle. It also corresponds to a wave number far
from the potential. While not strictly required, the integral Schrödinger
equation above tends to be most suited for particles in infinite
space.
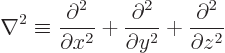
![]()