|
|
|
|
|
Next: 10.6 Nearly-Free Electrons |
|
Chapter 6 discussed the model of noninteracting electrons in a periodic box. This simple model, due to Sommerfeld, is a first starting point for much analysis of solids. It was used to provide explanations of such effects as the incompressibility of solids and liquids, and of electrical conduction. This section will use the model to explain some of the analytical methods that are used to analyze electrons in crystals. A free-electron gas is a model for electrons in a crystal when the physical effect of the crystal structure on the electrons is ignored. The assumption is that the crystal structure is still there, but that it does not actually do anything to the electrons.
The single-particle energy eigenfunctions of a periodic box are given
by
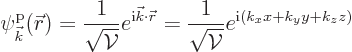 |
(10.11) |
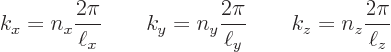 |
(10.12) |
Note that each of these eigenfunctions can be regarded as a Bloch wave: the exponentials are the Floquet ones, and the periodic parts are trivial constants. The latter reflects the fact the periodic potential itself is trivially constant (zero) for a free-electron gas.
Of course, there is a spin-up version ![]()
![]()
The Floquet exponentials have not been shifted to any first Brillouin zone. In fact, since the electrons experience no forces, as far as they are concerned, there is no crystal structure, hence no Brillouin zones.
As far as the mathematics of free electrons is concerned, the box in which they are confined may as well be empty. However,it is useful to put the results in context of a surrounding crystal lattice anyway. That will allow some of the basic concepts of the solid mechanics of crystals to be defined within a simple setting.
It will therefore be assumed that there is a crystal lattice, but that its potential is zero. So the lattice does not affect the motion of the electrons. An appropriate choice for this lattice must now be made. The plan is to keep the same Floquet wave number vectors as for the free electrons in a rectangular periodic box. Those wave numbers form a rectangular grid in wave number space as shown in figure 6.17 of chapter 6.18. To preserve these wave numbers, it is best to figure out a suitable reciprocal lattice first.
To do so, compare the general expression for the Fourier
![]()
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,19...
...0)[t]{$k_x$}}
\put(-2,187){\makebox(0,0)[r]{$k_y$}}
\end{picture}
\end{figure}](img2225.gif) |
In particular, if it is assumed that there are an equal number of
cells in each primitive direction, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
Note that in this section, the wave number space will be shown only in
the ![]()
![]()
A lattice like the one shown in figure 10.16 is called a
“simple cubic lattice,” and it is the easiest lattice that you
can define. The primitive vectors are orthonormal, just a multiple of
the Cartesian unit vectors ![]() ,
,![]() ,
,![]() .
.
It is of course not that strange that the simple cubic lattice would work here, because the assumed wave number vectors were derived for electrons in a rectangular periodic box.
How about the physical lattice? That is easy too. The simple cubic
lattice is its own reciprocal. So the physical crystal too consists
of cubic cells stacked together. (Atomic scale ones, of course, for a
physical lattice.) In particular, the wave numbers as shown in figure
10.16 correspond to a crystal that is macroscopically a
cube with equal sides ![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() .
.![]() ,
,![]()
In ![]() -
-![]()
It should be pointed out that the simple cubic lattice, while definitely simple, is not that important physically unless you happen to be particularly interested in polonium or compounds like cesium chloride or beta brass. But the mathematics is really no different for other crystal structures, just messier, so the simple cubic lattice makes a good example. Furthermore, many other lattices feature cubic unit cells, even if these cells are a bit larger than the primitive cell. That means that the assumption of a potential that has cubic periodicity on an atomic scale is quite widely applicable.
The previous subsection chose the reciprocal lattice in wave number space to be the simple cubic one. The next question is how the occupied states show up in it. As usual, it will be assumed that the crystal is in the ground state, corresponding to zero absolute temperature.
As shown in figure 6.17, in the ground state the energy levels occupied by electrons form a sphere in wave number space. The surface of the sphere is the Fermi surface. The corresponding single-electron energy is the Fermi energy.
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(400,52...
...0)[t]{$k_x$}}
\put(-2,161){\makebox(0,0)[r]{$k_y$}}
\end{picture}
\end{figure}](img2230.gif) |
Figure 10.17 shows the occupied states in ![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
However, these results may show up presented in a different way in
literature. The reason is that a Bloch-wave representation is not
unique. In terms of Bloch waves, the free-electron exponential
solutions as used here can be represented in the form
This free-electron way of thinking about the solutions is often not
the best way to understand the physics. Seen within a single physical
lattice cell, a solution with a Floquet wave number in a Wigner-Seitz
cell far from the origin looks like an extremely rapidly varying
exponential. However, all of that atom-scale physics is in the
crystal-scale Floquet exponential; the lattice-cell scale part
![]()
![]() .
.![]()
Now each Floquet wave number vector in the first Brillouin zone does
no longer correspond to just one spatial energy eigenfunction like in
the extended zone scheme. There will now be multiple spatial
eigenfunctions, distinguished by different lattice-scale variations
![]() .
.![]()
But you might rightly feel that the critical Fermi surface is messed up pretty badly in the reduced zone scheme figure 10.18b. That does not seem to be such a hot idea, since the electrons near the Fermi surface are critical for the properties of metals. However, the picture can now be taken apart again to produce separate Brillouin zones. There is a construction credited to Harrison that is illustrated in figure 10.18c. For points that are covered by at least one fragment of the original sphere, (which means all points, here,) the first covering is moved into the first Brillouin zone. For points that are covered by at least two fragments of the original sphere, the second covering is moved into the second Brillouin zone. And so on.
Remember that in say electrical conduction, the electrons change occupied states near the Fermi surfaces. To simplify talking about that, physicist like to extend the pictures of the Brillouin zones periodically, as illustrated in figure 10.19. This is called the “periodic zone scheme.” In this scheme, the boundaries of the Wigner-Seitz cells, which are normally not Fermi surfaces, are no longer a distracting factor. It may be noted that a bit of a lattice potential will round off the sharp corners in figure 10.19, increasing the esthetics.