13.3 Ex­am­ple Sta­tic Elec­tro­mag­netic Fields

In this sec­tion, some ba­sic so­lu­tions of Maxwell’s equa­tions are de­scribed. They will be of in­ter­est in ad­den­dum {A.39} for un­der­stand­ing rel­a­tivis­tic ef­fects on the hy­dro­gen atom (though cer­tainly not es­sen­tial). They are also of con­sid­er­able prac­ti­cal im­por­tance for a lot of non­quan­tum ap­pli­ca­tions.

It is as­sumed through­out this sub­sec­tion that the elec­tric and mag­netic fields do not change with time. All so­lu­tions also as­sume that the am­bi­ent medium is vac­uum.

Ta­ble 13.1: Elec­tro­mag­net­ics I: Fun­da­men­tal equa­tions and ba­sic so­lu­tions.

Ta­ble 13.2: Elec­tro­mag­net­ics II: Elec­tro­mag­ne­to­sta­tic so­lu­tions.

For easy ref­er­ence, Maxwell’s equa­tions and var­i­ous re­sults to be ob­tained in this sec­tion are col­lected to­gether in ta­bles 13.1 and 13.2. While the ex­is­tence of mag­netic monopoles is un­ver­i­fied, it is of­ten con­ve­nient to com­pute as if they do ex­ist. It al­lows you to ap­ply ideas from the elec­tric field to the mag­netic field and vice-versa. So, the ta­bles in­clude mag­netic monopoles with strength $q_m$, in ad­di­tion to elec­tric charges with strength $q$, and a mag­netic cur­rent den­sity $\vec\jmath_m$ in ad­di­tion to an elec­tric cur­rent den­sity $\vec\jmath$. The ta­ble uses the per­mit­tiv­ity of space $\epsilon_0$ and the speed of light $c$ as ba­sic phys­i­cal con­stants; the per­me­abil­ity of space $\mu_0$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1$\raisebox{.5pt}{$/$}$​$\epsilon_0c^2$ is just an an­noy­ance in quan­tum me­chan­ics and is avoided. The ta­ble has been writ­ten in terms of $c\skew2\vec{\cal B}$ and $\vec\jmath_m$$\raisebox{.5pt}{$/$}$​$c$ be­cause in terms of those com­bi­na­tions Maxwell’s equa­tions have a very pleas­ing sym­me­try. It al­lows you to eas­ily con­vert be­tween ex­pres­sions for the elec­tric and mag­netic fields. You wish that physi­cists would have de­fined the mag­netic field as $c\skew2\vec{\cal B}$ in­stead of $\skew2\vec{\cal B}$ in SI units, but no such luck.

13.3.1 Point charge at the ori­gin

A point charge is a charge con­cen­trated at a sin­gle point. It is a very good model for the elec­tric field of the nu­cleus of an atom, since the nu­cleus is so small com­pared to the atom. A point charge of strength $q$ lo­cated at the ori­gin has a charge den­sity

$$\mbox{point charge at the origin:}\quad \rho({\skew0\vec r}) = q \delta^3({\skew0\vec r})$$ (13.13)

where $\delta^3({\skew0\vec r})$ is the three-di­men­sion­al delta func­tion. A delta func­tion is a spike at a sin­gle point that in­te­grates to one, so the charge den­sity above in­te­grates to the to­tal charge $q$.

The elec­tric field lines of a point charge are ra­di­ally out­ward from the charge; see for ex­am­ple fig­ure 13.3 in the pre­vi­ous sub­sec­tion. Ac­cord­ing to Coulomb’s law, the elec­tric field of a point charge is

$$\fbox{$\displaystyle \mbox{electric field of a point charg... ...\vec{\cal E}= \frac{q}{4\pi\epsilon_0r^2} {\hat\imath}_r $} %$$ (13.14)

where $r$ is the dis­tance from the charge, ${\hat\imath}_r$ is the unit vec­tor point­ing straight away from the charge, and $\epsilon_0$ $\vphantom0\raisebox{1.5pt}{$=$}$ 8.85 10$\POW9,{-12}$ C$\POW9,{2}$/J m is the per­mit­tiv­ity of space. Now for sta­tic elec­tric charges the elec­tric field is mi­nus the gra­di­ent of a po­ten­tial $\varphi$,

$$\skew3\vec{\cal E}= - \nabla\varphi \qquad \nabla \equiv ... ...c{\partial}{\partial y} + {\hat k}\frac{\partial}{\partial z}$$

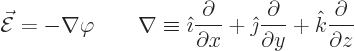
In every­day terms the po­ten­tial $\varphi$ is called the volt­age. It fol­lows by in­te­gra­tion of the elec­tric field strength with re­spect to $r$ that the po­ten­tial of a point charge is

$$\fbox{$\displaystyle \mbox{electric potential of a point charge:}\quad \varphi=\frac{q}{4\pi\epsilon_0r} $} %$$ (13.15)

Mul­ti­ply by $\vphantom{0}\raisebox{1.5pt}{$-$}$$e$ and you get the po­ten­tial en­ergy $V$ of an elec­tron in the field of the point charge. That was used in writ­ing the Hamil­to­ni­ans of the hy­dro­gen and heav­ier atoms.

Delta func­tions are of­ten not that easy to work with an­a­lyt­i­cally, since they are in­fi­nite and in­fin­ity is a tricky math­e­mat­i­cal thing. It is of­ten eas­ier to do the math­e­mat­ics by as­sum­ing that the charge is spread out over a small sphere of ra­dius $\varepsilon$, rather than con­cen­trated at a sin­gle point. If it is as­sumed that the charge dis­tri­b­u­tion is uni­form within the ra­dius $\varepsilon$, then it is

$$\mbox{spherical charge around the origin:}\quad \rho = \l... ...isplaystyle 0 &\mbox{if } r > \varepsilon \end{array} \right.$$ (13.16)

Since the charge den­sity is the charge per unit vol­ume, the charge den­sity times the vol­ume $\frac43\pi\varepsilon^3$ of the lit­tle sphere that holds it must be the to­tal charge $q$. The ex­pres­sion above makes it so.

Fig­ure 13.7: Elec­tric field and po­ten­tial of a charge that is dis­trib­uted uni­formly within a small sphere. The dot­ted lines in­di­cate the val­ues for a point charge.

Fig­ure 13.7 shows that out­side the re­gion with charge, the elec­tric field and po­ten­tial are ex­actly like those of a point charge with the same net charge $q$. But in­side the re­gion of charge dis­tri­b­u­tion, the elec­tric field varies lin­early with ra­dius, and be­comes zero at the cen­ter. It is just like the grav­ity of earth: go­ing above the sur­face of the earth out into space, grav­ity de­creases like 1$\raisebox{.5pt}{$/$}$​$r^2$ if $r$ is the dis­tance from the cen­ter of the earth. But if you go down be­low the sur­face of the earth, grav­ity de­creases also and be­comes zero at the cen­ter of the earth. If you want, you can de­rive the elec­tric field of the spher­i­cal charge from Maxwell’s first equa­tion; it goes much in the same way that Coulomb’s law was de­rived from it in the pre­vi­ous sec­tion.

If mag­netic monopoles ex­ist, they would cre­ate a mag­netic field much like an elec­tric charge cre­ates an elec­tric field. As ta­ble 13.1 shows, the only dif­fer­ence is the square of the speed of light $c$ pop­ping up in the ex­pres­sions. (And that is re­ally just a mat­ter of de­f­i­n­i­tions, any­way.) In real life, these ex­pres­sions give an ap­prox­i­ma­tion for the mag­netic field near the north or south pole of a very long thin mag­net as long as you do not look in­side the mag­net.

Fig­ure 13.8: Elec­tric field of a two-di­men­sional line charge.

A ho­mo­ge­neous dis­tri­b­u­tion of charges along an in­fi­nite straight line is called a line charge. As shown in fig­ure 13.8, it cre­ates a two-di­men­sion­al field in the planes nor­mal to the line. The line charge be­comes a point charge within such a plane. The ex­pres­sion for the field of a line charge can be de­rived in much the same way as Coulomb’s law was de­rived for a three-di­men­sion­al point charge in the pre­vi­ous sec­tion. In par­tic­u­lar, where that de­riva­tion sur­rounded the point charge by a spher­i­cal sur­face, sur­round the line charge by a cylin­der. (Or by a cir­cle, if you want to think of it in two di­men­sions.) The re­sult­ing ex­pres­sions are given in ta­ble 13.1; they are in terms of the charge per unit length of the line $q'$. Note that in this sec­tion a prime is used to in­di­cate that a quan­tity is per unit length.

13.3.2 Dipoles

A point charge can de­scribe a sin­gle charged par­ti­cle like an atom nu­cleus or elec­tron. But much of the time in physics, you are deal­ing with neu­tral atoms or mol­e­cules. For those, the net charge is zero. The sim­plest model for a sys­tem with zero net charge is called the di­pole. It is sim­ply a com­bi­na­tion of a pos­i­tive point charge $q$ and a neg­a­tive one $\vphantom{0}\raisebox{1.5pt}{$-$}$$q$, mak­ing the net charge zero.

Fig­ure 13.9: Field lines of a ver­ti­cal elec­tric di­pole.

Fig­ure 13.9 shows an ex­am­ple of a di­pole in which the pos­i­tive charge is straight above the neg­a­tive one. Note the dis­tinc­tive egg shape of the biggest elec­tric field lines. The elec­tric di­pole mo­ment $\vec\wp$ is de­fined as the prod­uct of the charge strength $q$ times the con­nect­ing vec­tor from neg­a­tive to pos­i­tive charge:

$$\mbox{electric dipole moment:}\quad \vec\wp = q ({\skew0\vec r}_\oplus-{\skew0\vec r}_\ominus) %$$ (13.17)

where ${\skew0\vec r}_\oplus$ and ${\skew0\vec r}_\ominus$ are the po­si­tions of the pos­i­tive and neg­a­tive charges re­spec­tively.

The po­ten­tial of a di­pole is sim­ply the sum of the po­ten­tials of the two charges:

$$\mbox{potential of an electric dipole:}\quad \varphi = \fr... ... \frac{1}{\vert{\skew0\vec r}-{\skew0\vec r}_{\ominus}\vert} %$$ (13.18)

Note that to con­vert the ex­pres­sions for a charge at the ori­gin to one not at the ori­gin, you need to use the po­si­tion vec­tor mea­sured from the lo­ca­tion of the charge.

The elec­tric field of the di­pole can be found from ei­ther tak­ing mi­nus the gra­di­ent of the po­ten­tial above, or from adding the fields of the in­di­vid­ual point charges, and is

$$\mbox{field of an electric dipole:}\quad \skew3\vec{\cal E}... ...minus}}{\vert{\skew0\vec r}-{\skew0\vec r}_{\ominus}\vert^3} %$$ (13.19)

To ob­tain that re­sult from tak­ing the the gra­di­ent of the po­ten­tial, re­mem­ber the fol­low­ing im­por­tant for­mula for the gra­di­ent of $\vert{\skew0\vec r}-{\skew0\vec r}_0\vert^n$ with $n$ an ar­bi­trary power:

$$\fbox{$\displaystyle \frac{\partial\vert{\skew0\vec r}-{\s... ...w0\vec r}_0\vert^{n-2} ({\skew0\vec r}-{\skew0\vec r}_0) $} %$$ (13.20)

The first ex­pres­sion gives the gra­di­ent in in­dex no­ta­tion and the sec­ond gives it in vec­tor form. The sub­script on $\nabla$ merely in­di­cates that the dif­fer­en­ti­a­tion is with re­spect to ${\skew0\vec r}$, not ${\skew0\vec r}_0$. These for­mu­lae will be used rou­tinely in this sec­tion. Us­ing them, you can check that mi­nus the gra­di­ent of the di­pole po­ten­tial does in­deed give its elec­tric field above.

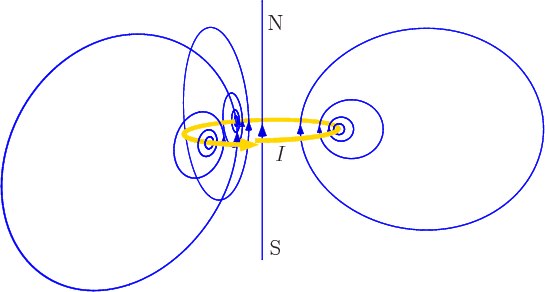
Sim­i­lar ex­pres­sions ap­ply for mag­netic dipoles. The field out­side a thin bar mag­net can be ap­prox­i­mated as a mag­netic di­pole, with the north and south poles of the mag­net as the pos­i­tive and neg­a­tive mag­netic point charges. The mag­netic field lines are then just like the elec­tric field lines in fig­ure 13.9.

Fig­ure 13.10: Elec­tric field of a two-di­men­sional di­pole.

Cor­re­spond­ing ex­pres­sions can also be writ­ten down in two di­men­sions, for op­po­site charges dis­trib­uted along par­al­lel straight lines. Fig­ure 13.10 gives an ex­am­ple. In two di­men­sions, all field lines are cir­cles pass­ing through both charges.

A par­ti­cle like an elec­tron has an elec­tric charge and no known size. It can there­fore be de­scribed as an ideal point charge. But an elec­tron also has a mag­netic mo­ment: it acts as a mag­net of zero size. Such a mag­net of zero size will be re­ferred to as an “ideal mag­netic di­pole.” More pre­cisely, an ideal mag­netic di­pole is de­fined as the limit of a mag­netic di­pole when the two poles are brought van­ish­ingly close to­gether. Now if you just let the two poles ap­proach each other with­out do­ing any­thing else, their op­po­site fields will be­gin to in­creas­ingly can­cel each other, and there will be no field left when the poles are on top of each other. When you make the dis­tance be­tween the poles smaller, you also need to in­crease the strengths $q_m$ of the poles to en­sure that the

$$\mbox{magnetic dipole moment:}\quad \vec\mu = q_m ({\skew0\vec r}_\oplus-{\skew0\vec r}_\ominus)$$ (13.21)

re­mains fi­nite. So you can think of an ideal mag­netic di­pole as in­fi­nitely strong mag­netic poles in­fi­nitely close to­gether.

Fig­ure 13.11: Field of an ideal mag­netic di­pole.

The field lines of a ver­ti­cal ideal mag­netic di­pole are shown in fig­ure 13.11. Their egg shape is in spher­i­cal co­or­di­nates de­scribed by, {D.72},

$$r = r_{\rm max} \sin^2\theta \qquad \phi = \mbox{constant} %$$ (13.22)

To find the mag­netic field it­self, start with the mag­netic po­ten­tial of a non­ideal di­pole,

$$\varphi_m = \frac{q_m}{4\pi\epsilon_0c^2} \left[ \frac{1}{... ...1}{\vert{\skew0\vec r}-{\skew0\vec r}_{\ominus}\vert} \right]$$

Now take the neg­a­tive pole at the ori­gin, and al­low the pos­i­tive pole to ap­proach it van­ish­ingly close. Then the po­ten­tial above takes the generic form

$$\varphi_m = f({\skew0\vec r}-{\skew0\vec r}_{\oplus}) - f({... ...rac{q_m}{4\pi\epsilon_0c^2} \frac{1}{\vert{\skew0\vec r}\vert}$$

Now ac­cord­ing to the to­tal dif­fer­en­tial of cal­cu­lus, (or the multi-di­men­sion­al Tay­lor se­ries the­o­rem, or the de­f­i­n­i­tion of di­rec­tional de­riv­a­tive), for small ${\skew0\vec r}_{\oplus}$ an ex­pres­sion of the form $f({\skew0\vec r}-{\skew0\vec r}_{\oplus})-f({\skew0\vec r})$ can be ap­prox­i­mated as

$$f({\skew0\vec r}-{\skew0\vec r}_{\oplus}) - f({\skew0\vec r... ...ot\nabla f \quad\mbox{for}\quad {\skew0\vec r}_{\oplus} \to 0$$

From this the mag­netic po­ten­tial of an ideal di­pole at the ori­gin can be found by us­ing the ex­pres­sion (13.20) for the gra­di­ent of 1$\raisebox{.5pt}{$/$}$​$\vert{\skew0\vec r}\vert$ and then sub­sti­tut­ing the mag­netic di­pole strength $\vec\mu$ for $q_m{\skew0\vec r}_{\oplus}$. The re­sult is

$$\mbox{potential of an ideal magnetic dipole:}\quad \varphi_... ...1}{4\pi\epsilon_0c^2} \frac{\vec\mu\cdot{\skew0\vec r}}{r^3} %$$ (13.23)

The cor­re­spond­ing mag­netic field can be found as mi­nus the gra­di­ent of the po­ten­tial, us­ing again (13.20) and the fact that the gra­di­ent of $\vec\mu\cdot{\skew0\vec r}$ is just $\vec\mu$:

$$\skew2\vec{\cal B}= \frac{1}{4\pi\epsilon_0c^2} \frac{3(\vec\mu\cdot{\skew0\vec r}){\skew0\vec r}-\vec\mu r^2}{r^5} %$$ (13.24)

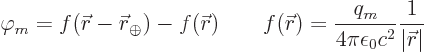
Sim­i­lar ex­pres­sions can be writ­ten down for ideal elec­tric dipoles and in two-di­men­sions. They are listed in ta­bles 13.1 and 13.2. (The delta func­tions will be dis­cussed in the next sub­sec­tion.)

Fig­ure 13.12: Elec­tric field of an al­most ideal two-di­men­sional di­pole.

Fig­ure 13.12 shows an al­most ideal two-di­men­sion­al elec­tric di­pole. The spac­ing be­tween the charges has been re­duced sig­nif­i­cantly com­pared to that in fig­ure 13.10, and the strength of the charges has been in­creased. For two-di­men­sion­al ideal dipoles, the field lines in a cross-plane are cir­cles that all touch each other at the di­pole.

13.3.3 Ar­bi­trary charge dis­tri­b­u­tions

Mod­el­ing elec­tric sys­tems like atoms and mol­e­cules and their ions as sin­gu­lar point charges or dipoles is not very ac­cu­rate, ex­cept in a de­tailed quan­tum so­lu­tion. In a clas­si­cal de­scrip­tion, it is more rea­son­able to as­sume that the charges are smeared out over space into a dis­tri­b­u­tion. In that case, the charges are de­scribed by the charge per unit vol­ume, called the charge den­sity $\rho$. The in­te­gral of the charge den­sity over vol­ume then gives the net charge,

$$q_{\rm region} = \int_{\rm region} \rho({\underline{\skew0\vec r}}) { \rm d}^3{\underline{\skew0\vec r}}$$ (13.25)

As far as the po­ten­tial is con­cerned, each lit­tle piece $\rho({\underline{\skew0\vec r}}){ \rm d}^3{\underline{\skew0\vec r}}$ of the charge dis­tri­b­u­tion acts like a point charge at the point ${\underline{\skew0\vec r}}$. The ex­pres­sion for the po­ten­tial of such a point charge is like that of a point charge at the ori­gin, but with ${\skew0\vec r}$ re­placed by ${\skew0\vec r}-{\underline{\skew0\vec r}}$. The to­tal po­ten­tial re­sults from in­te­grat­ing over all the point charges. So, for a charge dis­tri­b­u­tion,

$$\varphi({\skew0\vec r}) = \frac{1}{4\pi\epsilon_0} \int_{{\... ...derline{\skew0\vec r}}){ \rm d}^3{\underline{\skew0\vec r}} %$$ (13.26)

The elec­tric field and sim­i­lar ex­pres­sion for mag­netic charge dis­tri­b­u­tions and in two di­men­sions may be found in ta­ble 13.2

Note that when the in­te­gral ex­pres­sion for the po­ten­tial is dif­fer­en­ti­ated to find the elec­tric field, as in ta­ble 13.2, the in­te­grand be­comes much more sin­gu­lar at the point of in­te­gra­tion where ${\underline{\skew0\vec r}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ ${\skew0\vec r}$. This may be of im­por­tance in nu­mer­i­cal work, where the more sin­gu­lar in­te­grand can lead to larger er­rors. It may then be a bet­ter idea not to dif­fer­en­ti­ate un­der the in­te­gral, but in­stead put the de­riv­a­tive of the charge den­sity in the in­te­gral, like in

$${\cal E}_x = - \frac{\partial \varphi}{\partial x} = - \fr... ...partial {\underline x}} { \rm d}^3{\underline{\skew0\vec r}}$$

and sim­i­lar for the $y$ and $z$ com­po­nents. That you can do that may be ver­i­fied by not­ing that dif­fer­en­ti­at­ing ${\skew0\vec r}-{\underline{\skew0\vec r}}$ with re­spect to $x$ is within a mi­nus sign the same as dif­fer­en­ti­at­ing with re­spect to ${\underline x}$, and then you can use in­te­gra­tion by parts to move the de­riv­a­tive to $\rho$.

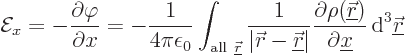
Now con­sider the case that the charge dis­tri­b­u­tion is re­stricted to a very small re­gion around the ori­gin, or equiv­a­lently, that the charge dis­tri­b­u­tion is viewed from a very large dis­tance. For sim­plic­ity, as­sume the case that the charge dis­tri­b­u­tion is re­stricted to a small re­gion around the ori­gin. In that case, ${\underline{\skew0\vec r}}$ is small wher­ever there is charge; the in­te­grand can there­fore be ap­prox­i­mated by a Tay­lor se­ries in terms of ${\underline{\skew0\vec r}}$ to give:

$$\varphi = \frac{1}{4\pi\epsilon_0} \int_{{\rm all }{\under... ...nderline{\skew0\vec r}}) { \rm d}^3{\underline{\skew0\vec r}}$$

where (13.20) was used to eval­u­ate the gra­di­ent of 1$\raisebox{.5pt}{$/$}$​$\vert{\underline{\skew0\vec r}}-{\skew0\vec r}\vert$ with re­spect to ${\underline{\skew0\vec r}}$.

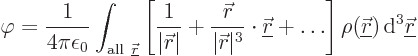
Since the frac­tions no longer in­volve ${\underline{\skew0\vec r}}$, they can be taken out of the in­te­grals and so the po­ten­tial sim­pli­fies to

$$\varphi = \frac{q}{4\pi\epsilon_0} \frac{1}{r} + \frac{1}{... ...derline{\skew0\vec r}}){ \rm d}^3{\underline{\skew0\vec r}} %$$ (13.27)

The lead­ing term shows that a dis­trib­uted charge dis­tri­b­u­tion will nor­mally look like a point charge lo­cated at the ori­gin when seen from a suf­fi­cient dis­tance. How­ever, if the net charge $q$ is zero, like hap­pens for a neu­tral atom or mol­e­cule, it will look like an ideal di­pole, the sec­ond term, when seen from a suf­fi­cient dis­tance.

The ex­pan­sion (13.27) is called a “mul­ti­pole ex­pan­sion.” It al­lows the ef­fect of a com­pli­cated charge dis­tri­b­u­tion to be de­scribed by a few sim­ple terms, as­sum­ing that the dis­tance from the charge dis­tri­b­u­tion is suf­fi­ciently large that its small scale fea­tures can be ig­nored. If nec­es­sary, the ac­cu­racy of the ex­pan­sion can be im­proved by us­ing more terms in the Tay­lor se­ries. Now re­call from the pre­vi­ous sec­tion that one ad­van­tage of Maxwell’s equa­tions over Coulomb’s law is that they al­low you to de­scribe the elec­tric field at a point us­ing purely lo­cal quan­ti­ties, rather than hav­ing to con­sider the charges every­where. But us­ing a mul­ti­pole ex­pan­sion, you can sim­plify the ef­fects of dis­tant charge dis­tri­b­u­tions. Then Coulomb’s law can be­come com­pet­i­tive with Maxwell’s equa­tions, es­pe­cially in cases where the charge dis­tri­b­u­tion is re­stricted to a rel­a­tively lim­ited frac­tion of the to­tal space.

The pre­vi­ous sub­sec­tion dis­cussed how an ideal di­pole could be cre­ated by de­creas­ing the dis­tance be­tween two op­po­site charges with a com­pen­sat­ing in­crease in their strength. The mul­ti­pole ex­pan­sion above shows that the same ideal di­pole is ob­tained for a con­tin­u­ous charge dis­tri­b­u­tion, pro­vided that the net charge $q$ is zero.

The elec­tric field of this ideal di­pole can be found as mi­nus the gra­di­ent of the po­ten­tial. But cau­tion is needed; the so-ob­tained elec­tric field may not be suf­fi­cient for your needs. Con­sider the fol­low­ing ball­park es­ti­mates. As­sume that the charge dis­tri­b­u­tion has been con­tracted to a typ­i­cal small size $\varepsilon$. Then the net pos­i­tive and neg­a­tive charges will have been in­creased by a cor­re­spond­ing fac­tor 1/$\varepsilon$. The elec­tric field within the con­tracted charge dis­tri­b­u­tion will then have a typ­i­cal mag­ni­tude 1/$\varepsilon\vert{\underline{\skew0\vec r}}-{\skew0\vec r}\vert^2$, and that means 1/$\varepsilon^3$, since the typ­i­cal size of the re­gion is $\varepsilon$. Now a quan­tity of or­der 1$\raisebox{.5pt}{$/$}$​$\varepsilon^3$ can in­te­grate to a fi­nite amount even if the vol­ume of in­te­gra­tion is small of or­der $\varepsilon^3$. In other words, there seems to be a pos­si­bil­ity that the elec­tric field may have a delta func­tion hid­den within the charge dis­tri­b­u­tion when it is con­tracted to a point. And so it does. The cor­rect delta func­tion is de­rived in de­riva­tion {D.72} and shown in ta­ble 13.2. It is im­por­tant in ap­pli­ca­tions in quan­tum me­chan­ics where you need some in­te­gral of the elec­tric field; if you for­get about the delta func­tion, you will get the wrong re­sult.

13.3.4 So­lu­tion of the Pois­son equa­tion

The pre­vi­ous sub­sec­tions stum­bled onto the so­lu­tion of an im­por­tant math­e­mat­i­cal prob­lem, the Pois­son equa­tion. The Pois­son equa­tion is

$$\nabla^2 \varphi = f$$ (13.28)

where $f$ is a given func­tion and $\varphi$ is the un­known one to be found. The Lapla­cian $\nabla^2$ is also of­ten found writ­ten as $\Delta$.

The rea­son that the pre­vi­ous sub­sec­tion stum­bled on to the so­lu­tion of this equa­tion is that the elec­tric po­ten­tial $\varphi$ sat­is­fies it. In par­tic­u­lar, mi­nus the gra­di­ent of $\varphi$ gives the elec­tric field; also, the di­ver­gence of the elec­tric field gives ac­cord­ing to Maxwell’s first equa­tion the charge den­sity $\rho$ di­vided by $\epsilon_0$. Put the two to­gether and it says that $\nabla^2\varphi$ $\vphantom0\raisebox{1.5pt}{$=$}$ $-\rho$$\raisebox{.5pt}{$/$}$​$\epsilon_0$. So, iden­tify the func­tion $f$ in the Pois­son equa­tion with $-\rho$$\raisebox{.5pt}{$/$}$​$\epsilon_0$, and there you have the so­lu­tion of the Pois­son equa­tion.

Be­cause it is such an im­por­tant prob­lem, it is a good idea to write out the ab­stract math­e­mat­i­cal so­lu­tion with­out the “phys­i­cal en­tourage” of (13.26):

$$\nabla^2\varphi=f \quad\Longrightarrow\quad \varphi({\skew... ...({\skew0\vec r}) = - \frac{1}{4\pi \vert{\skew0\vec r}\vert} %$$ (13.29)

The func­tion $G({\skew0\vec r}-{\underline{\skew0\vec r}})$ is called the Green’s func­tion of the Lapla­cian. It is the so­lu­tion for $\varphi$ if the func­tion $f$ is a delta func­tion at point ${\underline{\skew0\vec r}}$. The in­te­gral so­lu­tion of the Pois­son equa­tion can there­fore be un­der­stood as di­vid­ing func­tion $f$ up into spikes $f({\underline{\skew0\vec r}}){ \rm d}^3{\underline{\skew0\vec r}}$; for each of these spikes the con­tri­bu­tion to $\varphi$ is given by cor­re­spond­ing Green's func­tion.

It also fol­lows that ap­ply­ing the Lapla­cian on the Green’s func­tion pro­duces the three-di­men­sion­al delta func­tion,

$$\nabla^2 G({\skew0\vec r}) = \delta^3({\skew0\vec r}) \qqua... ...({\skew0\vec r}) = - \frac{1}{4\pi \vert{\skew0\vec r}\vert} %$$ (13.30)

with $\vert{\skew0\vec r}\vert$ $\vphantom0\raisebox{1.5pt}{$=$}$ $r$ in spher­i­cal co­or­di­nates. That some­times pops up in quan­tum me­chan­ics, in par­tic­u­lar in per­tur­ba­tion the­ory. You might ob­ject that the Green’s func­tion is in­fi­nite at ${\skew0\vec r}$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0, so that its Lapla­cian is un­de­fined there, rather than a delta func­tion spike. And you would be per­fectly right; just say­ing that the Lapla­cian of the Green’s func­tion is the delta func­tion is not re­ally jus­ti­fied. How­ever, if you slightly round the Green’s func­tion near ${\skew0\vec r}$ $\vphantom0\raisebox{1.5pt}{$=$}$ 0, say like $\varphi$ was rounded in fig­ure 13.7, its Lapla­cian does ex­ist every­where. The Lapla­cian of this rounded Green’s func­tion is a spike con­fined to the re­gion of round­ing, and it in­te­grates to one. (You can see the lat­ter from ap­ply­ing the di­ver­gence the­o­rem on a sphere en­clos­ing the re­gion of round­ing.) If you then con­tract the re­gion of round­ing to zero, this spike be­comes a delta func­tion in the limit of no round­ing. Un­der­stood in this way, the Lapla­cian of the Green’s func­tion is in­deed a delta func­tion.

The mul­ti­pole ex­pan­sion for a charge dis­tri­b­u­tion can also be con­verted to purely math­e­mat­i­cal terms:

$$\varphi = - \frac{1}{4\pi r} \int_{{\rm all }{\underline{\... ...kew0\vec r}}){ \rm d}^3{\underline{\skew0\vec r}} + \ldots %$$ (13.31)

(Of course, delta func­tions are in­fi­nite ob­jects, and you might won­der at the math­e­mat­i­cal rigor of the var­i­ous ar­gu­ments above. How­ever, there are solid ar­gu­ments based on “Green’s sec­ond in­te­gral iden­tity” that avoid the in­fini­ties and pro­duce the same fi­nal re­sults.)

13.3.5 Cur­rents

Streams of mov­ing elec­tric charges are called cur­rents. The cur­rent strength $I$ through an elec­tric wire is de­fined as the amount of charge flow­ing through a cross sec­tion per unit time. It equals the amount of charge $q'$ per unit length times its ve­loc­ity $v$;

$$I \equiv q' v %$$ (13.32)

The cur­rent den­sity $\vec\jmath$ is de­fined as the cur­rent per unit vol­ume, and equals the charge den­sity times the charge ve­loc­ity. In­te­grat­ing the cur­rent den­sity over the cross sec­tion of a wire gives its cur­rent.

Fig­ure 13.13: Mag­netic field lines around an in­fi­nite straight elec­tric wire.

As shown in fig­ure 13.13, elec­tric wires are en­cir­cled by mag­netic field lines. The strength of this mag­netic field may be com­puted from Maxwell’s fourth equa­tion. To do so, take an ar­bi­trary field line cir­cle. The field strength is con­stant on the line by sym­me­try. So the in­te­gral of the field strength along the line is just $2{\pi}r{\cal B}$; the perime­ter of the field line times its mag­netic strength. Now the Stokes’ the­o­rem of cal­cu­lus says that this in­te­gral is equal to the curl of the mag­netic field in­te­grated over the in­te­rior of the field line cir­cle. And Maxwell’s fourth equa­tion says that that is 1$\raisebox{.5pt}{$/$}$​$\epsilon_0c^2$ times the cur­rent den­sity in­te­grated over the cir­cle. And the cur­rent den­sity in­te­grated over the cir­cle is just the cur­rent through the wire. Put it all to­gether to get

$$\mbox{magnetic field of an infinite straight wire:}\quad {\cal B}= \frac{I}{2\pi\epsilon_0c^2r} %$$ (13.33)

Fig­ure 13.14: An elec­tro­mag­net con­sist­ing of a sin­gle wire loop. The gen­er­ated mag­netic field lines are in blue.

An in­fi­nite straight wire is of course not a prac­ti­cal way to cre­ate a mag­netic field. In a typ­i­cal elec­tro­mag­net, the wire is spooled around an iron bar. Fig­ure 13.14 shows the field pro­duced by a sin­gle wire loop, in vac­uum. To find the fields pro­duced by curved wires, use the so-called “Biot-Savart law” listed in ta­ble 13.2 and de­rived in {D.72}. You need it when you end up writ­ing a book on quan­tum me­chan­ics and have to plot the field.

Fig­ure 13.15: A cur­rent di­pole.

Of course, while fig­ure 13.14 does not show it, you will also need a lead from your bat­tery to the elec­tro­mag­net and a sec­ond lead back to the other pole of the bat­tery. These two leads form a two-di­men­sion­al cur­rent di­pole, as shown in fig­ure 13.15, and they pro­duce a mag­netic field too. How­ever, the cur­rents in the two leads are op­po­site; one com­ing from the bat­tery and other re­turn­ing to it, so the mag­netic fields that they cre­ate are op­po­site. There­fore, if you strand the wires very closely to­gether, their mag­netic fields will can­cel each other, and not mess up that of your elec­tro­mag­net.

It may be noted that if you bring the wires close to­gether, what­ever is left of the field has cir­cu­lar field lines that touch at the di­pole. In other words, a hor­i­zon­tal ideal cur­rent di­pole pro­duces the same field as a two-di­men­sion­al ver­ti­cal ideal charge di­pole. Sim­i­larly, the hor­i­zon­tal wire loop, if small enough, pro­duces the same field lines as a three-di­men­sion­al ver­ti­cal ideal charge di­pole. (How­ever, the delta func­tions are dif­fer­ent, {D.72}.)

13.3.6 Prin­ci­ple of the elec­tric mo­tor

The pre­vi­ous sec­tion dis­cussed how Maxwell’s third equa­tion al­lows elec­tric power gen­er­a­tion us­ing me­chan­i­cal means. The con­verse is also pos­si­ble; elec­tric power al­lows me­chan­i­cal power to be gen­er­ated; that is the prin­ci­ple of the elec­tric mo­tor.

Fig­ure 13.16: Elec­tric mo­tor us­ing a sin­gle wire loop. The Lorentz forces (black vec­tors) ex­erted by the ex­ter­nal mag­netic field on the elec­tric cur­rent car­ri­ers in the wire pro­duce a net mo­ment $M$ on the loop. The self-in­duced mag­netic field of the wire and the cor­re­spond­ing ra­dial forces are not shown.

It is pos­si­ble be­cause of the Lorentz force law, which says that a charge $q$ mov­ing with ve­loc­ity $\vec{v}$ in a mag­netic field $\skew2\vec{\cal B}$ ex­pe­ri­ences a force push­ing it side­ways equal to

$$\vec F = q \vec v \times \skew2\vec{\cal B}$$

Con­sider the wire loop in an ex­ter­nal mag­netic field sketched in fig­ure 13.16. The side­ways forces on the cur­rent car­ri­ers in the wire pro­duce a net mo­ment $\vec{M}$ on the wire loop that al­lows it to per­form use­ful work.

Fig­ure 13.17: Vari­ables for the com­pu­ta­tion of the mo­ment on a wire loop in a mag­netic field.

To be more pre­cise, the forces caused by the com­po­nent of the mag­netic field nor­mal to the wire loop are ra­dial and pro­duce no net force nor mo­ment. How­ever, the forces caused by the com­po­nent of the mag­netic field par­al­lel to the loop pro­duce forces nor­mal to the plane of the loop that do gen­er­ate a net mo­ment. Us­ing spher­i­cal co­or­di­nates aligned with the wire loop as in fig­ure 13.17, the com­po­nent of the mag­netic field par­al­lel to the loop equals ${\cal B}_{\rm {ext}}\sin\theta$. It causes a side­ways force on each el­e­ment $r{\rm d}\phi$ of the wire equal to

$${\rm d}F = \underbrace{q'r{\rm d}\phi}_{{\rm d}q} \underb... ...eta\sin\phi} _{\vec v\times\skew2\vec{\cal B}_{\rm parallel}}$$

where $q'$ is the net charge of cur­rent car­ri­ers per unit length and $v$ their ve­loc­ity. The cor­re­spond­ing net force in­te­grates to zero. How­ever the mo­ment does not; in­te­grat­ing

$${\rm d}M = \underbrace{r \sin\phi}_{\rm arm} \underbrace{q... ...d}\phi v {\cal B}_{\rm {ext}}\sin\theta\sin\phi} _{\rm force}$$

pro­duces

$$M = \pi r^2 q' v {\cal B}_{\rm ext}\sin\theta$$

If the work $M{\rm d}\theta$ done by this mo­ment is for­mu­lated as a change in en­ergy of the loop in the mag­netic field, that en­ergy is

$$E_{\rm ext} = - \pi r^2 q' v {\cal B}_{\rm ext}\cos\theta$$

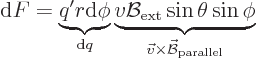
The mag­netic di­pole mo­ment $\vec\mu$ is de­fined as the fac­tor that only de­pends on the wire loop, in­de­pen­dent of the mag­netic field. In par­tic­u­lar $\mu$ $\vphantom0\raisebox{1.5pt}{$=$}$ ${\pi}r^2q'v$ and it is taken to be in the ax­ial di­rec­tion. So the mo­ment and en­ergy can be writ­ten more con­cisely as

$$\vec M = \vec\mu \times \skew2\vec{\cal B}_{\rm ext} \qquad E_{\rm ext} = - \vec\mu \cdot \skew2\vec{\cal B}_{\rm ext}$$

Yes, $\vec\mu$ also gov­erns how the mag­netic field looks at large dis­tances; feel free to ap­prox­i­mate the Biot-Savart in­te­gral for large dis­tances to check.

A book on elec­tro­mag­net­ics would typ­i­cally iden­tify $q'v$ with the cur­rent through the wire $I$ and ${\pi}r^2$ with the area of the loop, so that the mag­netic di­pole mo­ment is just $IA$. This is then valid for a flat wire loop of any shape, not just a cir­cu­lar one.

But this is a book on quan­tum me­chan­ics, and for elec­trons in or­bits about nu­clei, cur­rents and ar­eas are not very use­ful. In quan­tum me­chan­ics the more mean­ing­ful quan­tity is an­gu­lar mo­men­tum. So iden­tify $2{\pi}rq'$ as the to­tal elec­tric charge go­ing around in the wire loop, and mul­ti­ply that with the ra­tio $m_{\rm {c}}$$\raisebox{.5pt}{$/$}$​$q_{\rm {c}}$ of mass of the cur­rent car­rier to its charge to get the to­tal mass go­ing around. Then mul­ti­ply with $rv$ to get the an­gu­lar mo­men­tum $L$. In those terms, the mag­netic di­pole mo­ment is

$$\vec\mu = \frac{q_{\rm c}}{2m_{\rm c}} \vec L %$$ (13.34)

Usu­ally the cur­rent car­rier is an elec­tron, so $q_{\rm {c}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\vphantom{0}\raisebox{1.5pt}{$-$}$$e$ and $m_{\rm {c}}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $m_{\rm e}$.

These re­sults ap­ply to any ar­bi­trary cur­rent dis­tri­b­u­tion, not just a cir­cu­lar wire loop. For­mu­lae are in ta­ble 13.2 and gen­eral de­riva­tions in {D.72}.