| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.41 Derivation of the Einstein B coefficients
The purpose of this note is to derive the Einstein 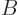 coefficients of
chapter 7.8. They determine the transition rates between
the energy states of atoms. For simplicity it will be assumed that
there are just two atomic energy eigenstates involved, a lower energy
one
coefficients of
chapter 7.8. They determine the transition rates between
the energy states of atoms. For simplicity it will be assumed that
there are just two atomic energy eigenstates involved, a lower energy
one 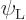 and an higher energy one
and an higher energy one 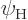 .
It is further assumed that the atoms are subject to incoherent ambient
electromagnetic radiation. The energy in the ambient radiation is
.
It is further assumed that the atoms are subject to incoherent ambient
electromagnetic radiation. The energy in the ambient radiation is
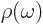 per unit volume and unit frequency range. Finally it
is assumed that the atoms suffer frequent collisions with other atoms.
The typical time between collisions will be indicated by
per unit volume and unit frequency range. Finally it
is assumed that the atoms suffer frequent collisions with other atoms.
The typical time between collisions will be indicated by
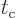 . It is small compared to the typical decay time of
the states, but large compared to the frequency of the relevant
electromagnetic field.
. It is small compared to the typical decay time of
the states, but large compared to the frequency of the relevant
electromagnetic field.
Unlike what you may find elsewhere, it will not be assumed that the
atoms are either fully in the high or fully in the low energy state.
That is a highly unsatisfactory assumption for many reasons. For one
thing it assumes that the atoms know what you have selected as
 -axis. In the derivation below, the atoms are allowed to be in a
linear combination of the states
-axis. In the derivation below, the atoms are allowed to be in a
linear combination of the states 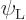 and
and
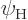 , with coefficients
, with coefficients 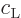 and
and
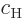 .
.
Since both the electromagnetic field and the collisions are random, a
statistical rather than a determinate treatment is needed. In it, the
probability that a randomly chosen atom can be found in the lower
energy state 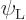 will be indicated by
will be indicated by 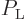 .
Similarly, the probability that an atom can be found in the higher
energy state
.
Similarly, the probability that an atom can be found in the higher
energy state 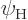 will be indicated by
will be indicated by 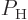 .
For a single atom, these probabilities are given by the square
magnitudes of the coefficients
.
For a single atom, these probabilities are given by the square
magnitudes of the coefficients 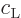 and
and 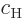 of the
energy states. Therefore,
of the
energy states. Therefore, 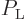 and
and 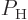 will be
defined as the averages of
will be
defined as the averages of 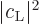 respectively
respectively
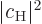 over all atoms.
over all atoms.
It is assumed that the collisions are globally elastic in the sense
that they do not change the average energy picture of the atoms. In
other words, they do not affect the average probabilities of the
eigenfunctions 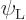 and
and 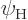 . However,
they are assumed to leave the wave function of an individual atom
immediately after a collision in some state
. However,
they are assumed to leave the wave function of an individual atom
immediately after a collision in some state
 in which
in which
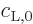 and
and 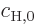 are quite random, especially with
respect to their phase. What is now to be determined in this note is
how, until the next collision, the wave function of the atom will
develop under the influence of the electromagnetic field and how that
changes the average probabilities
are quite random, especially with
respect to their phase. What is now to be determined in this note is
how, until the next collision, the wave function of the atom will
develop under the influence of the electromagnetic field and how that
changes the average probabilities 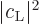 and
and
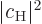 .
.
The evolution equations of the coefficients 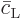 and
and
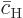 , in between collisions, were given in chapter
7.7.2 (7.42). They are in terms of modified
variables
, in between collisions, were given in chapter
7.7.2 (7.42). They are in terms of modified
variables 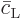 and
and 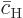 . However,
these variables have the same square magnitudes and initial conditions
as
. However,
these variables have the same square magnitudes and initial conditions
as 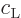 and
and 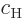 . So it really does not make a
difference.
. So it really does not make a
difference.
Further, because the equations are linear, the solution for the
coefficients 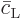 and
and 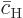 can be written
as a sum of two contributions, one proportional to the initial value
can be written
as a sum of two contributions, one proportional to the initial value
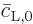 and the other to
and the other to 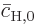 :
:
Here 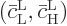 is the
solution that starts out from the lower energy state
is the
solution that starts out from the lower energy state
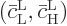

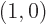 while
while 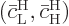 is the
solution that starts out from the higher energy state
is the
solution that starts out from the higher energy state
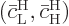

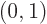 .
.
Now consider what happens to the probability of an atom to be in the
excited state in the time interval between collisions:
Here 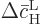 indicates the change in
indicates the change in
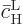 in the time interval between collisions;
in particular
in the time interval between collisions;
in particular
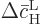

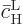 since
this solution starts from the ground state with
since
this solution starts from the ground state with
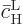
 0. Similarly, the change
0. Similarly, the change
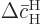 equals
equals
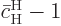 since this solution starts out from the
excited state with
since this solution starts out from the
excited state with 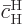
 1.
1.
Because the typical time between collisions 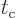 is assumed
small, so will be the changes
is assumed
small, so will be the changes 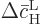 and
and
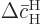 as given by the evolution
equations (7.42). Note also that
as given by the evolution
equations (7.42). Note also that
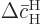 will be quadratically small, since
the corresponding solution starts out from
will be quadratically small, since
the corresponding solution starts out from 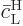
 0, so
0, so 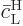 is an additional small factor
in the equation (7.42) for
is an additional small factor
in the equation (7.42) for
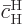 .
.
Therefore, if the change in probability  above
is multiplied out, ignoring terms that are cubically small or less,
the result is, (remember that for a complex number
above
is multiplied out, ignoring terms that are cubically small or less,
the result is, (remember that for a complex number 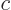 ,
, 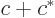 is twice its real part):
is twice its real part):
Now if this is averaged over all atoms and time intervals between
collisions, the first term in the right hand side will average away.
The reason is that it has a random phase angle, for one since those of
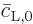 and
and 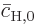 are assumed to be random
after a collision. For a number with a random phase angle, the real
part is just as likely to be positive as negative, so it averages
away. Also, for the final term,
are assumed to be random
after a collision. For a number with a random phase angle, the real
part is just as likely to be positive as negative, so it averages
away. Also, for the final term,
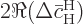 is the approximate change in
is the approximate change in
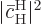 in the time interval, and that equals
in the time interval, and that equals
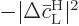 because of the normalization
condition
because of the normalization
condition
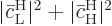
 1. So
the relevant expression for the average change in probability becomes
1. So
the relevant expression for the average change in probability becomes
Summing the changes in the probabilities therefore means summing the
changes in the square magnitudes of 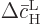 and
and 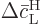 .
.
If the above expression for the average change in the probability of
the high energy state is compared to (7.46), it is seen
that the Einstein coefficient 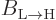 is the average change
is the average change
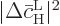 per unit time. This is
admittedly the same answer you would get if you assumed that the atoms
are either in the low energy state or in the high energy state
immediately after each collision. But as noted, that assumption is
simply not reasonable.
per unit time. This is
admittedly the same answer you would get if you assumed that the atoms
are either in the low energy state or in the high energy state
immediately after each collision. But as noted, that assumption is
simply not reasonable.
Now the needed
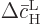

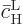 may be
found from the second evolution equation (7.42). To do so,
you can consider
may be
found from the second evolution equation (7.42). To do so,
you can consider 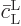 to be 1. The reason is
that it starts out as 1, and it never changes much because of the
assumed short evolution time
to be 1. The reason is
that it starts out as 1, and it never changes much because of the
assumed short evolution time 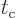 compared to the typical
transition time between states. That allows
compared to the typical
transition time between states. That allows
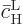 to be found from a simple integration.
And the second term in the modified Hamiltonian coefficient
(7.44) can be ignored because of the additional assumption
that
to be found from a simple integration.
And the second term in the modified Hamiltonian coefficient
(7.44) can be ignored because of the additional assumption
that 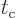 is still large compared to the frequency of the
electromagnetic wave. That causes the exponential in the second term
to oscillate rapidly and it does not integrate to a sizable
contribution.
is still large compared to the frequency of the
electromagnetic wave. That causes the exponential in the second term
to oscillate rapidly and it does not integrate to a sizable
contribution.
What is left is
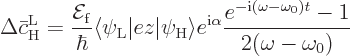 |
(D.25) |
and 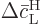 is given by a virtually
identical expression. However, since it is assumed that the atoms are
subject to incoherent radiation of all wave numbers
is given by a virtually
identical expression. However, since it is assumed that the atoms are
subject to incoherent radiation of all wave numbers 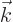 and
polarizations
and
polarizations 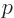 , the complete
, the complete
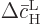 will consist of the sum of all their
contributions:
will consist of the sum of all their
contributions:
(This really assumes that the particles are in a very large periodic
box so that the electromagnetic field is given by a Fourier series; in
free space you would need to integrate over the wave numbers instead
of sum over them.) The square magnitude is then
where the final equality comes from the assumption that the radiation
is incoherent, so that the phases of different waves are uncorrelated
and the corresponding products average to zero.
The bottom line is that square magnitudes must be summed together to
find the total contribution of all waves. And the square magnitude of
the contribution of a single wave is, according to (D.25)
above,
Now broadband radiation is described in terms of an electromagnetic
energy density 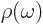 ; in particular
; in particular
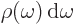 gives the energy per unit volume due to the
electromagnetic waves in an infinitesimal frequency range
gives the energy per unit volume due to the
electromagnetic waves in an infinitesimal frequency range 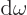 around a frequency
around a frequency 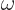 . For a single wave, this energy
equals
. For a single wave, this energy
equals 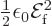 , chapter
13.2 (13.11).
And the square amplitudes of different waves simply add up to the
total energy; that is the so-called Parseval equality of Fourier
analysis. So to sum the expression above over all the frequencies
, chapter
13.2 (13.11).
And the square amplitudes of different waves simply add up to the
total energy; that is the so-called Parseval equality of Fourier
analysis. So to sum the expression above over all the frequencies
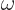 of the broadband radiation, make the substitution
of the broadband radiation, make the substitution
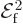

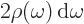

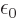 and integrate:
and integrate:
If a change of integration variable is made to 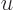

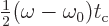 , the integral becomes
, the integral becomes
Recall that a starting assumption underlying these derivations was
that 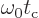 was large. So the lower limit of integration
can be approximated as
was large. So the lower limit of integration
can be approximated as 
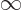 .
.
Note that this is essentially the same analysis as the one for
Fermi’s golden rule, except for the presence of the given field
strength 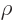 . However, here the mathematics can be performed
more straightforwardly, using integration rather than summation.
. However, here the mathematics can be performed
more straightforwardly, using integration rather than summation.
Consider for a second the limiting process that the field strength
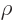 goes to zero, and that the atom is kept isolated enough that
the collision time
goes to zero, and that the atom is kept isolated enough that
the collision time 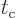 can increase correspondingly. Then
the term
can increase correspondingly. Then
the term 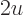

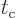 in the argument of
in the argument of 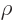 will tend to zero.
So only waves with the exact frequency
will tend to zero.
So only waves with the exact frequency 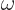

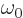 will produce
transitions in the limit of zero field strength. That confirms the
basic claim of quantum mechanics that only the energy eigenvalues are
measurable. In the absence of an electromagnetic field and other
disturbances, the energy eigenvalues are purely the atomic ones.
(Also recall that relativistic quantum mechanics adds that in reality,
the electric field is never zero.)
will produce
transitions in the limit of zero field strength. That confirms the
basic claim of quantum mechanics that only the energy eigenvalues are
measurable. In the absence of an electromagnetic field and other
disturbances, the energy eigenvalues are purely the atomic ones.
(Also recall that relativistic quantum mechanics adds that in reality,
the electric field is never zero.)
In any case, while the term 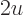

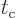 may not be exactly zero,
it is certainly small compared to
may not be exactly zero,
it is certainly small compared to 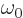 because of the assumption
that
because of the assumption
that 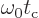 is large. So the term may be ignored
anyway. Then
is large. So the term may be ignored
anyway. Then 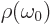 is a constant in the integration and
can be taken out. The remaining integral is in table books,
[41, 18.36], and the result is
is a constant in the integration and
can be taken out. The remaining integral is in table books,
[41, 18.36], and the result is
This must still be averaged over all directions of wave propagation
and polarization. That gives:
where
To see why, consider the electromagnetic waves propagating along any
axis, not just the 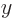 -axis, and polarized in either of the other two
axial directions. These waves will include
-axis, and polarized in either of the other two
axial directions. These waves will include 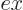 and
and 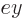 as well as
as well as
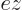 in the transition probability, making the average as shown above.
And of course, waves propagating in an oblique rather than axial
direction are simply axial waves when seen in a rotated coordinate
system and produce the same average.
in the transition probability, making the average as shown above.
And of course, waves propagating in an oblique rather than axial
direction are simply axial waves when seen in a rotated coordinate
system and produce the same average.
The Einstein coefficient 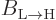 is the average change per
unit time, so the claimed (7.47) results from dividing by
the time
is the average change per
unit time, so the claimed (7.47) results from dividing by
the time 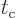 between collisions. There is no need to do
between collisions. There is no need to do
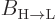 separately from
separately from
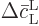 ; it follows immediately from
the symmetry property mentioned at the end of chapter 7.7.2
that it is the same.
; it follows immediately from
the symmetry property mentioned at the end of chapter 7.7.2
that it is the same.
![]()
![]()
![]() .
.![]()
![]() .
.![]() -
-![]()
![]() ,
,![]()
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]() :
:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
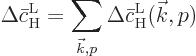
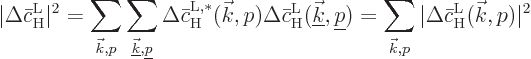
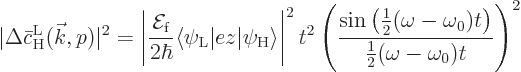
![]() ;
;![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
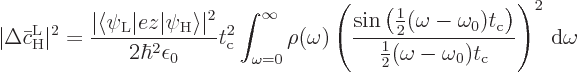
![]()
![]()
![]() ,
,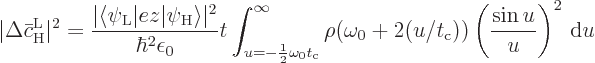
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
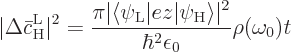
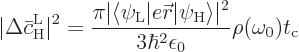
![]()
![]()
![]()
![]() ;
;