|
|
|
|
|
Next: 7.8 General Interaction with Radiation |
|
This section will address the basic physic of absorption and emission of radiation by a gas of atoms in an electromagnetic field. The next section will give practical formulae.
Figure 7.9 shows the three different processes of
interest. The previous sections already discussed the process of
spontaneous emission. Here an atom in a state ![]()
![]()
![]()
![]()
2
state, and the lower energy
state ![]()
![]()
![]()
1s
ground
state, as defined in chapter 4.3.
To a superb approximation, the photon carries off the difference in
energy between the atomic states. In view of the Planck-Einstein
relation, that means that its frequency ![]()
Unfortunately, the discussion of spontaneous emission in the previous sections had to remain incomplete. Nonrelativistic quantum mechanics as covered in this book cannot accommodate the creation of new particles like the photon in this case. The number of particles has to stay the same.
The second process of interest in figure 7.9 is
absorption. Here an atom in a low energy state ![]()
![]() .
.
The third process is stimulated emission. In this case an atom in an
excited state ![]()
![]() .
.
This process is the operating principle of lasers. Suppose that you bring a large number of atoms into a relatively stable excited state. Then suppose that one of the atoms performs a spontaneous emission. The photon released by that atom can stimulate another excited atom to release a photon too. Then there are two coherent photons, which can go on to stimulate still more excited atoms to release still more photons. And so on in an avalanche effect. It can produce a runaway process of photon release in which a macroscopic amount of monochromatic, coherent light is created.
Masers work on the same principle, but the radiation is of much lower energy than visible light. It is therefore usually referred to as microwaves instead of light. The ammonia molecule is one possible source of such low energy radiation, chapter 5.3.
The analysis in this section will illuminate some of the details of
stimulated emission. For example, it turns out that photon absorption
by the lower energy atoms, figure 7.9(b), competes on
a perfectly equal footing with stimulated emission, figure
7.9(c). If you have a 50/50 mixture of atoms in the
excited state ![]()
![]() ,
,
(Note that the lower energy state is not necessarily the same as the ground state. All else being the same, it obviously helps to have the lower energy state itself decay rapidly to a state of still lower energy. To a considerable extent, you can pick and choose decay rates, because decay rates can vary greatly depending on the amount to which they are forbidden, section 7.4.)
Key Points
- An electromagnetic field can cause atoms to absorb photons.
- However, it can also cause excited atoms to release photons. That is called stimulated emission.
- In lasers and masers, an avalanche effect of stimulated emission produces coherent, monochromatic light.
To describe the effect of an electromagnetic field on an atom using quantum mechanics, as always the Hamiltonian operator is needed.
The atom will be taken to be a hydrogen atom for simplicity. Since the proton is heavy, the electromagnetic field interacts mainly with the electron. The proton will be assumed to be at rest.
It is also necessary to simplify the electromagnetic field. That can be done by decomposing the field into separate “plane waves.” The total interaction can usually be obtained by simply summing the effects produced by the separate waves.
A single plane wave has an electric field ![]()
![]()
Fortunately, the expression for the wave can be greatly simplified.
The electron reacts primarily to the electric field, provided that its
kinetic energy is small compared to its rest mass energy. That is
certainly true for the electron in a hydrogen atom and for the outer
electrons of atoms in general. Therefore the magnetic field can be
ignored. (The error made in doing so is described more precisely in
{D.39}.) Also, the wave length of the electromagnetic
wave is usually much larger than the size of the atom. For example,
the Lyman-transition wave lengths are of the order of a thousand Å,
while the atom is about one Å. So, as far as the light wave is
concerned, the atom is just a tiny speck at the origin. That means
that ![]()
| (7.40) |
Now the question is how this field changes the Hamiltonian of the
electron. Ignoring the time dependence of the electric field, that is
easy. The Hamiltonian is
The interesting term is the second one, the perturbation caused by the
electromagnetic field. In this term ![]()
![]() -
-![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]() .
.
To be sure, the electric field is time dependent. The above
perturbation potential really assumes that “the electron moves
so fast that the field seems steady to it.” Indeed, if an
electron speed
is ballparked from its kinetic energy,
the electron does seem to travel through the atom relatively fast
compared to the frequency of the electric field. Of course, it is
much better to write the correct unsteady Hamiltonian and then show it
works out pretty much the same as the quasi-steady one above. That is
done in {D.39}.
Key Points
- An approximate Hamiltonian was written down for the interaction of an atom with an electromagnetic wave.
- By approximation the atom sees a uniform, quasi-steady electric field.
The big question is how the electromagnetic field affects transitions
between a typical atomic state ![]()
![]() .
.
The answer depends critically on various Hamiltonian coefficients. In
particular, the expectation values of the energies of the two states
are needed. They are
Note however that the two energies are now expectation values of energy; due to the electric field the atomic states develop uncertainty in energy. That is why they are no longer stationary states.
The other key Hamiltonian coefficient is
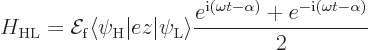
The next question is what these coeffients mean for the transitions
between two atomic states ![]()
![]() .
.
Evolution equations for these coefficients follow from the Schrödinger
equation. The way to find them was described in section
7.6, with additional manipulations in derivation
{D.38}. The resulting evolution equations are:
| (7.43) |
Note that this modified Hamiltonian coefficient is responsible for the
interaction between the states ![]()
![]() .
.
Whether this happens depends on whether the inner product
![]()
However, it does depend on the direction of the electric field. The
assumed plane wave had its electric field in the ![]() -
-![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.![]()
![]()
Note however that so-called forbidden transitions often occur just fine. The derivation in the previous subsection made several approximations, including that the magnetic field can be ignored and that the electric field is independent of position. If these ignored effects are corrected for, many forbidden transitions turn out to be possible after all; they are just much slower.
The approximations made to arrive at the atomic matrix element
![]()
electric dipole approximation.
The corresponding
transitions are called electric dipole transitions.
If
you want to know where the term comes from, why? Anyway, in that case
note first that if the electron charge distribution is symmetric
around the proton, the expectation value of ![]()
![]()
![]()
![]()
![]() .
.![]()
![]() -
-![]()
![]()
electric dipole transitions
is
justified, especially since basic electric transitions
would be understandable by far too many nonexperts.
Allowed and forbidden transitions were discussed earlier in section 7.4. However, that was based on assumed properties of the emitted photon. The allowed atomic matrix elements above, and similar forbidden ones, make it possible to check the various most important results directly from the governing equations. That is done in derivation {D.39}.
There is another requirement to get a decent transition probability. The exponentials in the modified Hamiltonian coefficient (7.44) must not oscillate too rapidly in time. Otherwise opposite values of the exponentials will average away against each other. So no significant transition probability can build up. (This is similar to the cancelation that gives rise to the adiabatic theorem, {D.34}.) Now under real-life conditions, the second exponential in (7.44) will always oscillate rapidly. Normal electromagnetic frequencies are very high. Therefore the second term in (7.44) can normally be ignored.
And in order for the first exponential not too oscillate too rapidly
requires a pretty good match between the frequencies ![]()
![]() .
.![]()
![]()
![]()
![]() .
.
One consequence is that in transitions between two atomic states
![]()
![]() ,
,![]()
![]() ,
,
In addition, the interest is often in the so-called
collision-dominated regime in which the atom evolves for only a short
time before being disturbed by collisions
with its
surroundings. In that case, the short evolution time prevents
nontrivial interactions between different transition processes to
build up. Transition rates for the individual transition processes
can be found separately and simply added together.
The obtained evolution equations (7.42) can explain why
absorption and stimulated emission compete on an equal footing in the
operation of lasers. The reason is that the equations have a
remarkable symmetry: for every solution ![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
An electromagnetic field that takes an atom out of the low energy stateIt is a consequence of the Hermitian nature of the Hamiltonian; it would not apply iftowards the high energy state will equally take that atom out of the high energy state towards the low energy state .
Key Points
- The governing evolution equations for the probabilities of two atomic states
and in an electromagnetic wave have been found.
- The equations have a symmetry property that makes electromagnetic waves equally effective for absorption and stimulated emission.
- Normally the electromagnetic field has no significant effect on transitions between the states unless its frequency
closely matches the frequency of a photon with energy .
- The governing equations can explain why some transitions are allowed and others are forbidden. The key are so-called
atomic matrix elements.