| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.44 Derivation of group velocity
The objective of this note is to derive the wave function for a wave
packet if time is large.
To shorten the writing, the Fourier integral (7.64) for
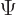 will be abbreviated as:
will be abbreviated as:
where it will be assumed that 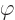 is a well behaved functions of
is a well behaved functions of
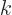 and
and  at least twice continuously differentiable. Note that the
wave number
at least twice continuously differentiable. Note that the
wave number 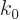 at which the group velocity equals
at which the group velocity equals 

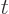 is a
stationary point for
is a
stationary point for 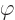 . That is the key to the
mathematical analysis.
. That is the key to the
mathematical analysis.
The so-called “method of stationary phase” says that the integral is
negligibly small as long as there are no stationary points
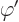
 0 in the range of integration. Physically that means that
the wave function is zero at large time positions that cannot be
reached with any group velocity within the range of the packet. It
therefore implies that the wave packet propagates with the group
velocity, within the variation that it has.
0 in the range of integration. Physically that means that
the wave function is zero at large time positions that cannot be
reached with any group velocity within the range of the packet. It
therefore implies that the wave packet propagates with the group
velocity, within the variation that it has.
To see why the integral is negligible if there are no stationary
points, just integrate by parts:
This is small of order 1
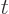 for large times. And if
for large times. And if
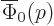 is chosen to smoothly become zero at the edges
of the wave packet, rather than abruptly, you can keep integrating by
parts to show that the wave function is much smaller still. That is
important if you have to plot a wave packet for some book on quantum
mechanics and want to have its surroundings free of visible
perturbations.
is chosen to smoothly become zero at the edges
of the wave packet, rather than abruptly, you can keep integrating by
parts to show that the wave function is much smaller still. That is
important if you have to plot a wave packet for some book on quantum
mechanics and want to have its surroundings free of visible
perturbations.
For large time positions with 

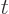 values within the range of
packet group velocities, there will be a stationary point to
values within the range of
packet group velocities, there will be a stationary point to
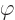 . The wave number at the stationary point will be
indicated by
. The wave number at the stationary point will be
indicated by 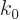 , and the value of
, and the value of 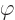 and its second
derivative by
and its second
derivative by 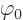 and
and 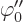 . (Note that the
second derivative is minus the first derivative of the group velocity,
and will be assumed to be nonzero in the analysis. If it would be
zero, nontrivial modifications would be needed.)
. (Note that the
second derivative is minus the first derivative of the group velocity,
and will be assumed to be nonzero in the analysis. If it would be
zero, nontrivial modifications would be needed.)
Now split the exponential in the integral into two,
It is convenient to write the difference in 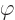 in terms of a
new variable
in terms of a
new variable 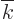 :
:
By Taylor series expansion it can be seen that 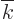 is a
well behaved monotonous function of
is a
well behaved monotonous function of 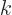 . The integral becomes
in terms
. The integral becomes
in terms 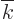 :
:
Now split function 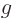 apart as in
apart as in
The part within brackets produces an integral
and integration by parts shows that to be small of order 1/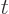 .
.
That leaves the first part, 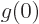

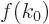 , which
produces
, which
produces
Change to a new integration variable
Note that since time is large, the limits of integration will be
approximately 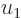


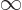 and
and 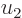

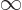 unless
the stationary point is right at an edge of the wave packet. The
integral becomes
unless
the stationary point is right at an edge of the wave packet. The
integral becomes
where 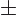 is the sign of
is the sign of 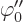 . The remaining
integral is a
. The remaining
integral is a Fresnel integral
that can be looked up
in a table book. Away from the edges of the wave packet, the
integration range can be taken as all 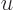 , and then
, and then
Convert back to the original variables and there you have the claimed
expression for the large time wave function.
Right at the edges of the wave packet, modified integration limits for
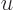 must be used, and the result above is not valid. In particular it
can be seen that the wave packet spreads out a distance of order
must be used, and the result above is not valid. In particular it
can be seen that the wave packet spreads out a distance of order
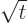 beyond the stated wave packet range; however, for large
times
beyond the stated wave packet range; however, for large
times 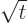 is small compared to the size of the wave packet,
which is proportional to
is small compared to the size of the wave packet,
which is proportional to 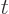 .
.
For the mathematically picky: the treatment above assumes that the
wave packet momentum range is not small in an asymptotic sense, (i.e.
it does not go to zero when 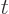 becomes infinite.) It is just small
in the sense that the group velocity must be monotonous. However,
Kaplun’s extension theorem implies that the packet size can be
allowed to become zero at least slowly. And the analysis is readily
adjusted for faster convergence towards zero in any case.
becomes infinite.) It is just small
in the sense that the group velocity must be monotonous. However,
Kaplun’s extension theorem implies that the packet size can be
allowed to become zero at least slowly. And the analysis is readily
adjusted for faster convergence towards zero in any case.
![]()
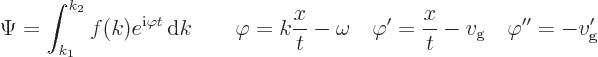
![]()
![]()
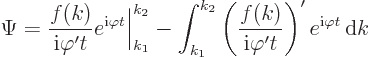
![]()
![]()
![]()
![]() .
.![]() ,
,![]()
![]()
![]() .
.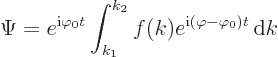
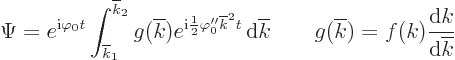
![]()
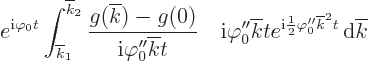
![]()
![]()
![]() ,
,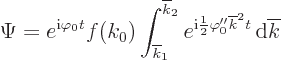
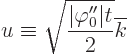
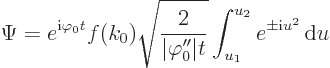
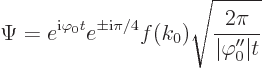
![]()
![]()
![]()
![]() .
.![]()