| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
D.45 Motion through crystals
This note derives the semi-classical motion of noninteracting
electrons in crystals. The derivations will be one-dimensional, but
the generalization to three dimensions is straightforward.
D.45.1 Propagation speed
The first question is the speed with which a more or less localized
electron moves. An electron in free space moves with a speed found by
dividing its linear momentum by its mass. However, in a solid, the
energy eigenfunctions are Bloch waves and these do not have
definite momentum.
Fortunately, the analysis for the wave packet of a free particle is
virtually unchanged for a particle whose energy eigenfunctions are
Bloch waves instead of simple exponentials. In the Fourier integral
(7.64), simply add the periodic factor
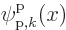 . Since this factor is periodic, it is
bounded, and it plays no part in limit process of infinite time. (You
can restrict the times in the limit process to those at which
. Since this factor is periodic, it is
bounded, and it plays no part in limit process of infinite time. (You
can restrict the times in the limit process to those at which  is
always at the same position in the period.)
is
always at the same position in the period.)
As a result the group velocity is again 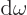

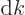 .
Since the energy is
.
Since the energy is 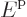

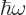 and the crystal momentum
and the crystal momentum
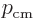

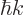 , the velocity of a localized
electron can be written as
, the velocity of a localized
electron can be written as
In the absence of external forces, the electron will keep moving with
the same velocity for all time. The large time wave function is
where 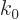 is the wave number at which the group speed equals
is the wave number at which the group speed equals


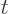 . Note that the wave function looks locally just like a
single Bloch wave for large time.
. Note that the wave function looks locally just like a
single Bloch wave for large time.
D.45.2 Motion under an external force
The acceleration due to an external force on an electrons is not that
straightforward. First of all note that you cannot just add a
constant external force. A constant force 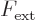 would
produce an external potential of the form
would
produce an external potential of the form 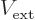

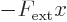 and that becomes infinite at infinite
and that becomes infinite at infinite  .
However, it can be assumed that the force is constant over the nonzero
range of the wave packet.
.
However, it can be assumed that the force is constant over the nonzero
range of the wave packet.
Next there is a trick. Consider the expectation value
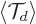 of the translation operator
of the translation operator 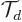 that
translates the wave function over one atomic cell size
that
translates the wave function over one atomic cell size 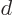 . If
the wave packet consisted of just a single Bloch wave with wave number
. If
the wave packet consisted of just a single Bloch wave with wave number
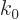 , the expectation value of
, the expectation value of 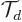 would be
would be
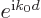 . A wave packet must however include a small
range of
. A wave packet must however include a small
range of 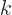 values. Then
values. Then 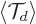 will be an
average of
will be an
average of 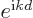 values over the
values over the 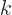 values of the wave
packet. Still, if the range of
values of the wave
packet. Still, if the range of 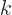 values is small enough, you can
write
values is small enough, you can
write
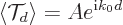
where 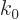 is a
is a 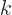 value somewhere in the middle of the wave packet
and
value somewhere in the middle of the wave packet
and  is a real number close to one. So
is a real number close to one. So 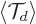 still gives the typical
still gives the typical 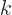 value in the wave packet.
value in the wave packet.
Moreover, its magnitude 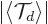

 is always
less than one and the closer it is to one, the more compact the wave
packet. That is because
is always
less than one and the closer it is to one, the more compact the wave
packet. That is because 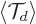 is an average of
is an average of
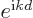 values. These are all located on the unit circle in the
complex plane, the plane with
values. These are all located on the unit circle in the
complex plane, the plane with 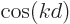 as the horizontal axis and
as the horizontal axis and
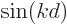 as the vertical axis. If the wave packet would consist of
just a single
as the vertical axis. If the wave packet would consist of
just a single 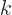 value
value 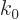 , then the average of
, then the average of 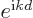 would be exactly
would be exactly 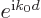 , and be on the unit circle. If
however the wave numbers spread out a bit around
, and be on the unit circle. If
however the wave numbers spread out a bit around 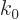 , then the
average moves inside the unit circle: if you average positions on a
circle, the average is always inside the circle. In the extreme case
that the
, then the
average moves inside the unit circle: if you average positions on a
circle, the average is always inside the circle. In the extreme case
that the 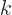 values get uniformly distributed over the entire circle,
the average position is at the origin. That would make
values get uniformly distributed over the entire circle,
the average position is at the origin. That would make
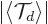 zero. Conversely, as long as
zero. Conversely, as long as
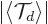 stays very close to one, the wave packet must
be very compact in terms of
stays very close to one, the wave packet must
be very compact in terms of 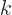 .
.
The time evolution of 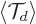 can be found using
chapter 7.2:
can be found using
chapter 7.2:
![\begin{displaymath}
\frac{{\rm d}\langle {\cal T}_d \rangle}{{\rm d}t} =
\frac...
...bar} \left\langle [H_0+V_{\rm {ext}},{\cal T}_d] \right\rangle
\end{displaymath}](img6862.gif) |
(D.28) |
where 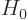 is the Hamiltonian for the electron in the crystal, and
is the Hamiltonian for the electron in the crystal, and
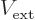 the additional external potential. Now the commutator
of
the additional external potential. Now the commutator
of 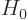 and
and 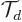 is zero; the crystal Hamiltonian acts
exactly the same on the wave function whether it is shifted one cell
over or not. The remainder of the commutator gives, when applied on
an arbitrary wave function,
is zero; the crystal Hamiltonian acts
exactly the same on the wave function whether it is shifted one cell
over or not. The remainder of the commutator gives, when applied on
an arbitrary wave function,
Writing this out with the arguments of the functions explicitly shown
gives:
Now assume that the external force 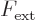 is constant over the
extent of the wave packet. In that case the difference in the
potentials is just
is constant over the
extent of the wave packet. In that case the difference in the
potentials is just 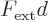 , and that is a constant that
can be taken out of the expectation value of the commutator. So:
, and that is a constant that
can be taken out of the expectation value of the commutator. So:
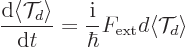 |
(D.29) |
The solution to this equation is:
where 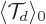 is the value of
is the value of
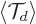 at the starting time
at the starting time 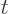
 0.
0.
It follows that the magnitude of the 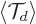 does not
change with time. In view of the earlier discussion, this means that
the wave packet maintains its compactness in terms of
does not
change with time. In view of the earlier discussion, this means that
the wave packet maintains its compactness in terms of 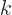 . (In
physical space the wave packet will gradually spread out, as can be
seen from the form of the large-time wave function given earlier.)
. (In
physical space the wave packet will gradually spread out, as can be
seen from the form of the large-time wave function given earlier.)
It further follows that the average wave number 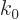 in the wave packet
evolves as:
in the wave packet
evolves as:
Since the packet remains compact, all wave numbers in the wave packet
change the same way. This is Newton’s second law in terms of
crystal momentum.
D.45.3 Free-electron gas with constant electric field
This book discussed the effect of an applied electric field on free
electrons in a periodic box in chapter 6.20. The effect
was described as a change of the velocity of the electrons. Since the
velocity is proportional to the wave number for free electrons, the
velocity change corresponds to a change in the wave number. In this
subsection the effect of the electric field will be examined in more
detail. The solution will again be taken to be one-dimensional, but
the extension to three dimensions is trivial.
Assume that a constant electric field is applied, so that the
electrons experience a constant force 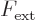 . The
time-dependent Schrödinger equation is
. The
time-dependent Schrödinger equation is
Assume the initial condition to be
in which a subscript 0 indicates the initial time.
The exact solution to this problem is
where the magnitude of the coefficients 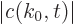

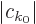 is
independent of time. This exact solution is in terms of states
is
independent of time. This exact solution is in terms of states
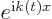 that change in time. The probability of the particle
being in those states does not change.
that change in time. The probability of the particle
being in those states does not change.
Unfortunately, this solution is only periodic with period equal to the
length of the box  for times at which
for times at which 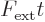

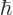 happens to be a whole multiple of the wave number spacing. At those
times the Fermi sphere of occupied states has shifted the same whole
multiple of wave number spacings to the right.
happens to be a whole multiple of the wave number spacing. At those
times the Fermi sphere of occupied states has shifted the same whole
multiple of wave number spacings to the right.
At intermediate times, the solution is not periodic, so it cannot be
correctly described using the periodic box modes. The magnitude of
the wave function is still periodic. However, the momentum has values
inconsistent with the periodic box. The problem is that even though a
constant force is periodic, the corresponding potential is not. Since
quantum mechanics uses the potential instead of the force, the quantum
solution is no longer periodic.
The problem goes away by letting the periodic box size become
infinite. But that brings back the ugly normalization problems. For
a periodic box, the periodic boundary conditions will need to be
relaxed during the application of the electric field. In particular,
a factor  difference in wave
function and its
difference in wave
function and its  -derivative must be allowed between the ends of
the box. Since the periodic boundary conditions are artificial anyway
for modeling a piece of electrical wire, this may not be a big
concern. In any case, for a big-enough periodic box, the times at
which the solution returns to its original periodicity become spaced
very close together.
-derivative must be allowed between the ends of
the box. Since the periodic boundary conditions are artificial anyway
for modeling a piece of electrical wire, this may not be a big
concern. In any case, for a big-enough periodic box, the times at
which the solution returns to its original periodicity become spaced
very close together.
![]() .
.![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]() ,
,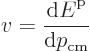
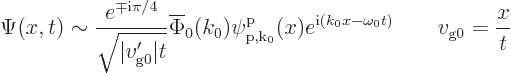
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]() ,
,![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
![]() .
.![]()
![]()
![]() ,
,![]()
![]() .
.![]()
![]() .
.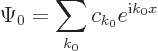
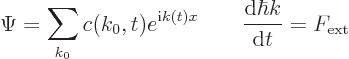
![]()
![]()
![]()
![]()
![]()
![]() -
-