| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.54 Derivation of the Hartree-Fock equations
This note derives the canonical Hartree-Fock equations. It will use
some linear algebra; see the Notations section under
matrix
for some basic concepts. The derivation will
be performed under the normally stated rules of engagement that the
orbitals are of the form 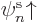 or
or 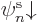 . So the spins
are chosen, and only the spatial orbitals
. So the spins
are chosen, and only the spatial orbitals 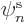 are to be
found.
are to be
found.
The derivations must allow for the fact that in restricted
Hartree-Fock, it is required that pairs of spin-up and spin-down
orbitals have the same spatial orbital. So there are three possible
kinds of spatial orbitals. A spatial orbital may produce a single
unpaired spin orbital that is spin-up, or a single unpaired spin
orbital that is spin-down, or a pair of spin-up and spin-down orbitals
with the same spatial orbital. These three types of spatial orbitals
will be referred to as unpaired spin-up, unpaired spin-down, and
restricted. Note that these names do not refer to properties of the
spatial orbits themselves, of course, but to the properties of the
spin orbits that these spatial orbitals produce.
Assume that there are 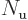 spin-up spatial orbitals,
spin-up spatial orbitals,
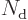 spin-down ones, and
spin-down ones, and 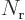 restricted ones. The
total number of spatial orbitals, call it N, is then
restricted ones. The
total number of spatial orbitals, call it N, is then
and that is the total number of unknown spatial orbitals to find. A
corresponding number of 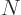 equations will be needed for them.
equations will be needed for them.
However, the total number of spin orbitals, 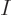 , is larger than
, is larger than
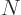 by an additional amount
by an additional amount 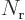 , because the restricted
spatial orbitals appear in both spin-up and spin-down versions. That
makes the mathematics messy.
, because the restricted
spatial orbitals appear in both spin-up and spin-down versions. That
makes the mathematics messy.
Things become a bit easier if the ordering of the orbitals is
specified a priori. The ordering makes no difference physically. So
it will be assumed that the spatial orbitals are ordered with the
unpaired spin-up ones first, the unpaired spin-down ones second, and
the restricted ones last. The ordering of the spin orbitals will be
the same as that of the spatial orbitals, but with the restricted
orbitals at the end appearing twice; first in the spin-up versions and
then in the spin-down versions.
To find the spatial orbitals, the variational method as discussed in
chapter 9.1.3 says that the expectation energy 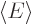 must be unchanged under small changes in the orbitals, provided that
the orbitals remain orthonormal. To easily enforce that
orthonormality constraint requires that terms are added to the change
in orbitals that penalize for any going out of bounds.
must be unchanged under small changes in the orbitals, provided that
the orbitals remain orthonormal. To easily enforce that
orthonormality constraint requires that terms are added to the change
in orbitals that penalize for any going out of bounds.
To do so, first note that 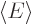 can be considered to be a real
function from the real and imaginary parts of the spatial orbitals,
and both these parts are real functions. The condition that any
spatial orbital
can be considered to be a real
function from the real and imaginary parts of the spatial orbitals,
and both these parts are real functions. The condition that any
spatial orbital 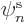 must be normalized means that the
inner product of the orbital with itself must be 1,
must be normalized means that the
inner product of the orbital with itself must be 1,
This condition is real too. However, the condition
that any spatial mode 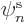 must be orthogonal to
any other spatial mode
must be orthogonal to
any other spatial mode 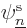 means that the inner product
of the two modes must be zero,
means that the inner product
of the two modes must be zero,
In general this condition has both a real and an imaginary component.
But it can be written as two real conditions;
The reason is that if you swap the sides in an inner product, you get
the complex conjugate; therefore the first equation above is the real
part of the inner product and the second the imaginary part.
Since we now have a completely real problem in real independent
variables, the penalty factors (the Lagrangian multipliers) in the
problem will be real too. For reasons evident in a second, the
penalty factor for the normalization condition above will be called
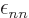 , while the ones for the two real orthogonality
conditions will be called
, while the ones for the two real orthogonality
conditions will be called 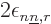 and
and
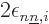 , respectively. To avoid enforcing the same
orthogonality condition twice, it is here assumed that
, respectively. To avoid enforcing the same
orthogonality condition twice, it is here assumed that 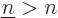 .
.
The reason for these notations is that in terms of them, the penalized
variational condition that the spatial orbitals must satisfy, chapter
9.1.3, takes the simple form
where 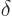 denotes a small change in the following quantity,
denotes a small change in the following quantity,
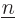 is now allowed to be both smaller or larger than
is now allowed to be both smaller or larger than  , and
, and
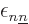 is a Hermitian matrix, meaning that
is a Hermitian matrix, meaning that
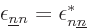
Note however that two spatial orbitals do not have to be orthogonal if
one is a unpaired spin-up one and the other an unpaired spin-down one.
In that case the spins take care of orthogonality. This can be
accomodated by stipulating that the penalty factors of the
corresponding constraints are zero,
Next the variational condition is to be evaluated for a small change
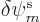 in a sample spatial wave function
in a sample spatial wave function 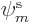 where
where 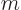 is no larger than
is no larger than 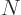 . This is straightforward for the
inner products in the penalty terms. However, the expectation value
of energy
. This is straightforward for the
inner products in the penalty terms. However, the expectation value
of energy 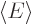 was obtained in chapter 9.3.3
in terms of the spin, rather than spatial orbitals:
was obtained in chapter 9.3.3
in terms of the spin, rather than spatial orbitals:
(From here on, the argument of the first orbital of a pair in either
side of an inner product is taken to be the first inner product
integration variable 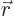 and the argument of the second orbital is
the second integration variable
and the argument of the second orbital is
the second integration variable 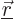 )
)
Taking that into account, the variational condition for the
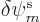 takes the messy form
takes the messy form
Here ![$[2?]$](img7062.gif) means to insert a factor 2 there if
means to insert a factor 2 there if 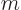 is one of
the restricted spatial orbitals, because each of the two corresponding
spin orbitals produces a term like that. And
is one of
the restricted spatial orbitals, because each of the two corresponding
spin orbitals produces a term like that. And
![$[\langle{\updownarrow}_.\vert{\updownarrow}_.\rangle^2?]$](img7063.gif) means leave away this inner
product if
means leave away this inner
product if 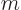 is one of the restricted spatial orbitals, because
exactly one of the two corresponding spin orbitals has that inner
product equal to one, and the other has it zero.
is one of the restricted spatial orbitals, because
exactly one of the two corresponding spin orbitals has that inner
product equal to one, and the other has it zero.
Note that the difference between 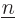 and
and  can from now on be
ignored; the name of a summation variable makes no difference for the
result, and there are no longer name conflicts in the individual
terms. Note also that the sums over
can from now on be
ignored; the name of a summation variable makes no difference for the
result, and there are no longer name conflicts in the individual
terms. Note also that the sums over  (or
(or 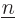 ) with upper limit
) with upper limit
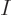 include the restricted spatial orbitals twice, once for
each spin direction.
include the restricted spatial orbitals twice, once for
each spin direction.
The second term in each row in the expression above is just the
complex conjugate of the first. These second terms can be thrown out
using the same trick as in chapter 9.1.3. (In other
words, average with the same equation with 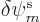 replaced
by
replaced
by 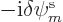 and divided by
and divided by 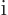 .) And the integrals
with the factors
.) And the integrals
with the factors 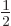 are pairwise the same; the difference is
just a name swap of the inner product integration variables. So all
there is really left is
are pairwise the same; the difference is
just a name swap of the inner product integration variables. So all
there is really left is
Now write out the inner product over the first position coordinate
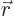 , being the argument of
, being the argument of 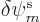 , for all terms:
, for all terms:
If this integral is to be zero for whatever is
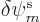 , then the terms within the parentheses must be
zero. (Otherwise just take
, then the terms within the parentheses must be
zero. (Otherwise just take  proportional to the
parenthetical expression; you would get the norm of the expression,
and that is only zero if the expression is.)
proportional to the
parenthetical expression; you would get the norm of the expression,
and that is only zero if the expression is.)
Unavoidably then, the following equations, one for each value of 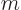 ,
must be satisfied:
,
must be satisfied:
This can be cleaned up a bit by dividing by [2?]:
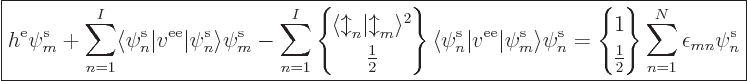 |
(D.35) |
These are the general Hartree-Fock equations, one for each 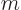
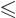
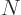 . The upper value between braces applies if the spatial orbital
. The upper value between braces applies if the spatial orbital
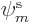 is not a restricted one; otherwise the lower value
applies. Recall that the sums with upper limit
is not a restricted one; otherwise the lower value
applies. Recall that the sums with upper limit 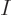 include the
restricted spatial orbitals twice. And that
include the
restricted spatial orbitals twice. And that 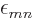 is zero
if spatial orbital
is zero
if spatial orbital 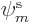 is unpaired spin-up and
is unpaired spin-up and 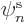 unpaired spin-down or vice-versa. For such index values,
unpaired spin-down or vice-versa. For such index values,
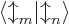 is zero too.
is zero too.
Note that the general Hartree-Fock equation above includes 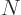
eigenvalues
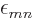 . The canonical equations
include just a single eigenvalue
. The canonical equations
include just a single eigenvalue 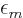 . So to get the
canonical Hartree-Fock equations, the sum in the right hand side must
be further simplified to the form
. So to get the
canonical Hartree-Fock equations, the sum in the right hand side must
be further simplified to the form 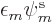 .
.
The restricted closed-shell Hartree-Fock case will be done first,
since it is the easiest one. Every spatial orbital is restricted, so
the lower choice in the curly brackets always applies. The summation
upper limits 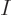 , being the number of spin orbitals, can be reduced to
the number of spatial orbitals
, being the number of spin orbitals, can be reduced to
the number of spatial orbitals 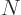 by adding a factor 2. We can also
get rid of the factor
by adding a factor 2. We can also
get rid of the factor 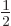 in front of the
in front of the 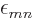 by
simply redefining them by that factor. So for restricted closed-shell
Hartree-Fock
by
simply redefining them by that factor. So for restricted closed-shell
Hartree-Fock
Now the reason why all these 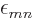 are there is because the
set of
are there is because the
set of 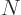 spatial orbitals that gives the lowest energy state are not
unique. The equation above applies to a typical set. Only a special
set will get rid of the
spatial orbitals that gives the lowest energy state are not
unique. The equation above applies to a typical set. Only a special
set will get rid of the 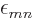 for
for  not equal to
not equal to 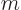 ,
leaving only
,
leaving only 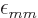 , which can then be defined to be
, which can then be defined to be
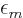 .
.
Each orbital in the special set will be some combination of the
orbitals in the typical set above. In particular, any orbital in the
special set, call it 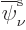 , will be a linear
combination of the orbitals
, will be a linear
combination of the orbitals 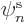 in the typical set as
follows:
in the typical set as
follows:
where the numbers 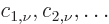 are the multiples of
the typical orbitals
are the multiples of
the typical orbitals 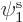 ,
, 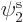 , .... The complete set
of numbers
, .... The complete set
of numbers 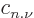 for all possible values of both
for all possible values of both  and
and 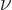 can be written as a
can be written as a matrix,
a table of numbers. This
matrix will be indicated by 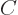 . The first index in
. The first index in 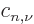 ,
,  ,
says what row in
,
says what row in 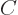 that coefficient is in, and the second index,
that coefficient is in, and the second index,
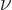 , what column.
, what column.
The multiples 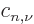 cannot be arbitrary, because the special
orbitals must still be orthonormal. As noted earlier, they will be if
they are normalized (so the inner product of any orbital with itself
is 1), and mutually orthogonal (so the inner product of any orbital
with any other one is zero). In short, the requirement is that
cannot be arbitrary, because the special
orbitals must still be orthonormal. As noted earlier, they will be if
they are normalized (so the inner product of any orbital with itself
is 1), and mutually orthogonal (so the inner product of any orbital
with any other one is zero). In short, the requirement is that
where 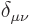 is one if
is one if 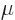

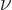 , and zero
otherwise. The set of numbers
, and zero
otherwise. The set of numbers 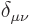 is called the
“Kronecker delta” or “unit matrix” or “identity matrix.” (The identity matrix is for matrices what the
number 1 is for normal numbers; multiplying an arbitrary matrix or
vector by the identity matrix does not change that matrix or vector.)
is called the
“Kronecker delta” or “unit matrix” or “identity matrix.” (The identity matrix is for matrices what the
number 1 is for normal numbers; multiplying an arbitrary matrix or
vector by the identity matrix does not change that matrix or vector.)
Substituting in the expression for the special orbitals above, making
sure not to use the same name 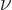 for two different indices, the
requirement becomes
for two different indices, the
requirement becomes
or noting that numbers come out of the left side of an inner product
as complex conjugates,
Now since the set of typical orbitals 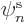 are already
orthonormal, the inner product in the requirement above is only
nonzero when
are already
orthonormal, the inner product in the requirement above is only
nonzero when 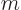 is
is  , and then it is one. So dropping the zero
terms that have
, and then it is one. So dropping the zero
terms that have 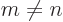 , the requirement on the coefficients
simplifies to
, the requirement on the coefficients
simplifies to
What does that mean? Well, for given values of 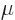 and
and 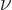 ,
consider the coefficients
,
consider the coefficients 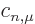 to form a vector
to form a vector 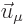 ,
where
,
where  indicates the component number of that vector. Similarly,
consider the coefficients
indicates the component number of that vector. Similarly,
consider the coefficients 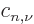 to form a vector
to form a vector 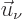 .
Then the left hand side in the requirement above is the inner (or dot,
if real) product of these two vectors. So the set of vectors must be
orthonormal, just like the special orbitals must be orthonormal. So
the matrix of coefficients
.
Then the left hand side in the requirement above is the inner (or dot,
if real) product of these two vectors. So the set of vectors must be
orthonormal, just like the special orbitals must be orthonormal. So
the matrix of coefficients 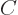 must consist of orthonormal vectors.
Mathematicians call such matrices “unitary,” rather than orthonormal, since it is easily confused
with
must consist of orthonormal vectors.
Mathematicians call such matrices “unitary,” rather than orthonormal, since it is easily confused
with unit,
and that keeps mathematicians in business
explaining all the confusion.
The Hermitian adjoint matrix 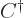 of
of 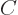 is defined as the
matrix you get by swapping the order of the indices of the elements of
is defined as the
matrix you get by swapping the order of the indices of the elements of
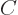 and adding a complex conjugate. So by definition the factor
and adding a complex conjugate. So by definition the factor
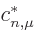 in the requirement above equals the coefficient
in the requirement above equals the coefficient
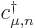 of
of 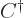 . And matrix multiplication is
defined such that then the sum over
. And matrix multiplication is
defined such that then the sum over  in the requirement gives
exactly the coefficients of the product
in the requirement gives
exactly the coefficients of the product 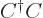 . So the
requirement above can be written as
. So the
requirement above can be written as
where 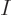 is the unit matrix. That means
is the unit matrix. That means 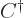 is the inverse
matrix to
is the inverse
matrix to 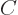 ,
, 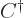

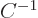 . Then you also have
that
. Then you also have
that 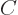 is the inverse of
is the inverse of 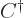 ,
, 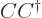

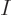 ,
which writes out to
,
which writes out to
This can be used to find the typical orbitals in terms of the special
ones. To do so, premultiply the expression for the special orbitals
as given earlier by 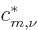 and sum over
and sum over 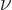 :
:
As seen above, the sum over 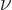 in the right hand side is just
in the right hand side is just
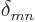 , so in the sum over
, so in the sum over  , only the term with
, only the term with  equal to
equal to
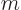 is nonzero:
is nonzero:
That then gives any typical orbital 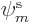 in terms of a sum of
the special orbitals
in terms of a sum of
the special orbitals 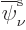 .
.
Now plug that into the non canonical restricted closed-shell
Hartree-Fock equations given earlier. Be careful not to use the same
summation index name twice in the same term; this derivation will use
for 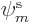 , the first occurrence of
, the first occurrence of 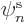 in the terms,
and the second occurrence, respectively. Premultiply it all by
in the terms,
and the second occurrence, respectively. Premultiply it all by 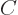 ,
i.e. put
,
i.e. put 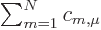 in front of each term. That cleans
up to
in front of each term. That cleans
up to
Note that the only thing that has changed more than just by symbol
names is the matrix in the right hand side. Now for each separate
value of 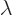 , take
, take 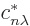 as the
as the 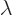 -th
orthonormal eigenvector of Hermitian matrix
-th
orthonormal eigenvector of Hermitian matrix 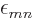 , calling
the eigenvalue
, calling
the eigenvalue 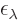 . Then by the definition of
eigenvector,
. Then by the definition of
eigenvector,
So the right hand side becomes
So, in terms of the special orbitals defined by the requirement that
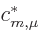 gives the
gives the 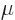 -th eigenvector of
-th eigenvector of 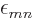 , the
right hand side simplifies to the canonical one.
, the
right hand side simplifies to the canonical one.
Since the old typical orbitals are no longer of interest, the
overlines on the special orbitals can be dropped to save typing, and
the Greek index names 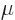 and
and 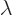 can be renamed
can be renamed  and
and
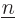 . That then finally produces the canonical closed-shell
restricted Hartree-Fock equations:
. That then finally produces the canonical closed-shell
restricted Hartree-Fock equations:
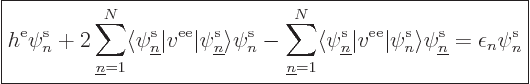 |
(D.36) |
Note that the left-hand side directly provides a Hermitian Fock
operator if you identify it as 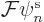 ; there is no need to
involve spin in the closed-shell restricted case. This also provides
a much simpler explanation than all the algebra above why all the
earlier
; there is no need to
involve spin in the closed-shell restricted case. This also provides
a much simpler explanation than all the algebra above why all the
earlier 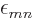 with
with 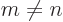 were not needed; existence of a
set of orthonormal eigenfunctions of a Hermitian operator is
automatic. So there is no fundamental need to enforce that
separately through Lagrangian multipliers.
were not needed; existence of a
set of orthonormal eigenfunctions of a Hermitian operator is
automatic. So there is no fundamental need to enforce that
separately through Lagrangian multipliers.
Turning now to the case of (fully) unrestricted Hartree-Fock (UHF),
you might make the same simple argument as above and be done. But it
is worthwhile to go through the full mathematics anyway, to better
understand open-shell restricted Hartree-Fock later. In the
unrestricted case, the non canonical equations are
In this case, there are two different types of spatial orbitals; those
appearing in spin-up spin orbitals, and those appearing in spin-down
spin orbitals. You cannot just make arbitrary combinations of all
these orbitals. If you combine spin-up and spin-down orbitals, they
correspond to spin orbitals of uncertain spin. That would make the
assumptions used to derive the Hartree-Fock equations invalid.
However, combinations of purely spin-up orbitals can still be made
without problems, and so can combinations of purely spin down
orbitals. To do the mathematics, the spatial orbitals can be
separated into two sets. The set of orbital numbers  corresponding
to spin-up spin orbitals will be indicated by U, and the set of
numbers
corresponding
to spin-up spin orbitals will be indicated by U, and the set of
numbers  corresponding to spin-down spin orbitals by D. So you can
partition (separate) the non canonical equations above into equations
for
corresponding to spin-down spin orbitals by D. So you can
partition (separate) the non canonical equations above into equations
for 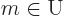 (meaning
(meaning 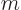 is one of the values in set U),
is one of the values in set U),
and equations for 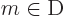 ,
,
In these two types of equations, the fact that the up and down spin
states are orthogonal was used to get rid of one pair of sums, and
another pair was eliminated by the fact that there are no Lagrangian
variables 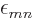 linking the sets, since the spatial orbitals
in the two sets are allowed to be mutually non orthogonal.
linking the sets, since the spatial orbitals
in the two sets are allowed to be mutually non orthogonal.
Now separately replace the orbitals of the up and down states by a
modified set just like for the restricted closed-shell case above, for
each using the unitary matrix of eigenvectors of the 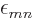 coefficients appearing in the right hand side of the equations for
that set. It leaves the equations intact except for changes in names,
but gets rid of the
coefficients appearing in the right hand side of the equations for
that set. It leaves the equations intact except for changes in names,
but gets rid of the 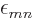 for
for 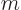
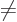
 , leaving only
, leaving only
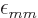 values, call them
values, call them 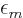 . Then combine the
spin-up and spin-down equations again into a single expression. You
get, in terms of revised symbol names,
. Then combine the
spin-up and spin-down equations again into a single expression. You
get, in terms of revised symbol names,
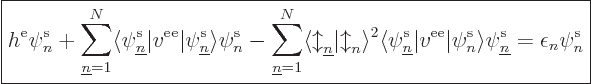 |
(D.37) |
That leaves only the restricted open-shell Hartree-Fock method. Here,
the partitioning also needs to include the set R of of restricted
orbitals besides U and D. There is now a problem, because you cannot
make combinations of restricted orbitals with spin-up or spin-down
orbitals. That means that the 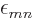 values where either
values where either 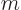 or
or  is restricted and the other is not, cannot be eliminated.
Solutions range from just ignoring the whole thing to properly
accounting for these
is restricted and the other is not, cannot be eliminated.
Solutions range from just ignoring the whole thing to properly
accounting for these 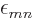 values by enforcing that
restricted and non restricted orbitals must stay orthogonal as
additional equations. This (even more) elaborate case will be left to
the references that you can find in [46], in
particular [28, pp. 242-253].
values by enforcing that
restricted and non restricted orbitals must stay orthogonal as
additional equations. This (even more) elaborate case will be left to
the references that you can find in [46], in
particular [28, pp. 242-253].
Woof.
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,![]() .
.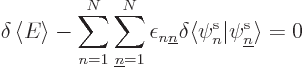
![]()
![]()
![]()
![]() .
.![]()
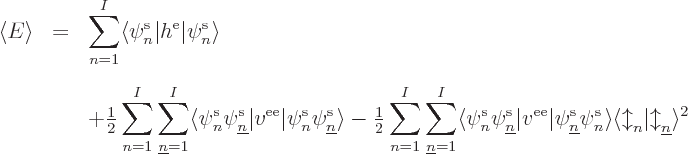
![]()
![\begin{eqnarray*}
&&
[2?]
\Big(
\langle\delta\pe m////\vert h^{\rm e}\vert\p...
...N \epsilon_{nm} \langle\pe n////\vert\delta\pe m////\rangle
= 0
\end{eqnarray*}](img7061.gif)
![]()
![]()
![]()
![]() )
)![]()
![]()
![]()
![]() .
.![]()
![\begin{eqnarray*}
&& [2?] \langle\delta\pe m////\vert h^{\rm e}\vert\pe m////\r...
...{n=1}^N \epsilon_{mn}\langle\delta\pe m////\vert\pe n////\rangle
\end{eqnarray*}](img7065.gif)
![]() ,
,![]() ,
,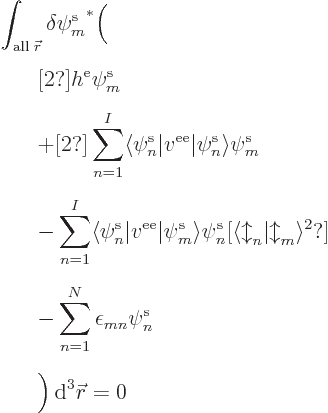
![]() ,
,![\begin{displaymath}[2?]h^{\rm e}\pe m////
+ [2?] \sum_{n=1}^I \langle\pe n////\...
... m////\rangle\pe n////
=
\sum_{n=1}^N \epsilon_{mn}\pe n////
\end{displaymath}](img7067.gif)
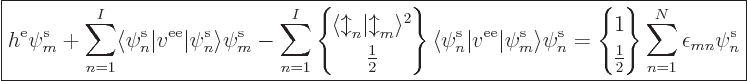
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]() .
.![]() .
.![]() ,
,![]()
![]()
![]()
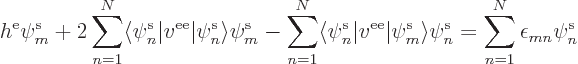
![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() .
.![]() ,
,![]()
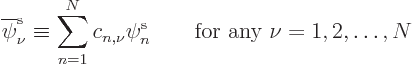
![]()
![]()
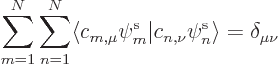
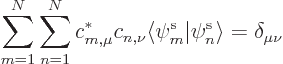
![]()
![]()
![]() ,
,![]() ,
,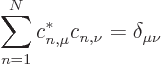
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.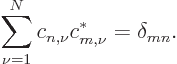
![]()
![]() :
: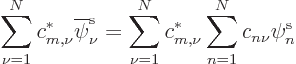
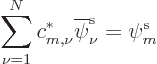
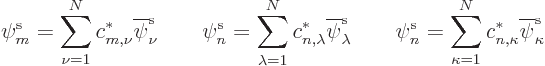
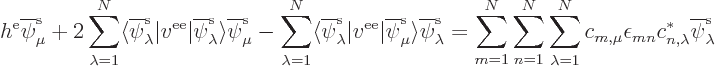
![]() ,
,![]()
![]() -
-![]() ,
,![]() .
.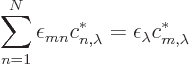
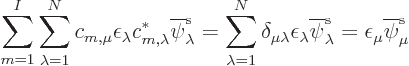
![]()
![]()
![]()
![]() .
.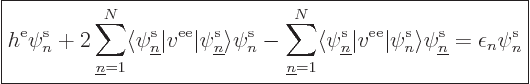
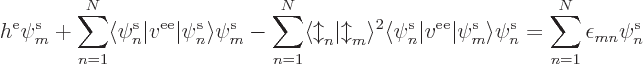
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() .
.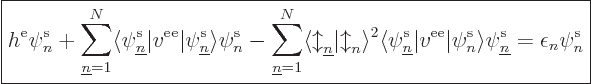
![]()
![]()
![]()
![]()