| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.53 Integral constraints
This note verifies the mentioned constraints on the Coulomb and
exchange integrals.
To verify that 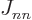

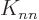 , just check their
definitions.
, just check their
definitions.
The fact that
is real and positive is self-evident, since it is an integral of a
real and positive function.
The fact that
is real can be seen by taking complex conjugate, and then noting that
the names of the integration variables do not make a difference, so
you can swap them.
The same name swap shows that 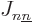 and
and 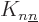 are symmetric
matrices;
are symmetric
matrices; 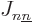

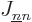 and
and 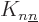

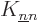 .
.
That 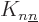 is positive is a bit trickier; write it as
is positive is a bit trickier; write it as
with 

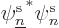 . The part within
parentheses is just the potential
. The part within
parentheses is just the potential 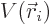 of a distribution of
charges with density
of a distribution of
charges with density 
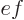 . Sure,
. Sure,  may be complex but
that merely means that the potential is too. The electric field is
minus the gradient of the potential,
may be complex but
that merely means that the potential is too. The electric field is
minus the gradient of the potential, 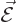


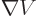 , and according to Maxwell’s equation, the
divergence of the electric field is the charge density divided by
, and according to Maxwell’s equation, the
divergence of the electric field is the charge density divided by
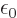 :
: 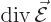


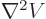


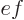

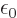 . So
. So 
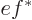

 and the integral is
and the integral is
and integration by parts shows it is positive. Or zero, if
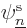 is zero wherever
is zero wherever 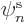 is not, and vice versa.
is not, and vice versa.
To show that 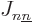
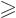
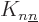 , note that
, note that
is nonnegative, for the same reasons as 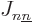 but with
but with
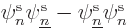 replacing
replacing
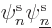 . If you multiply out the inner product,
you get that
. If you multiply out the inner product,
you get that 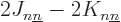 is nonnegative, so
is nonnegative, so 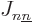
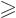
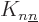 .
.
![]()
![]()
![]() ,
,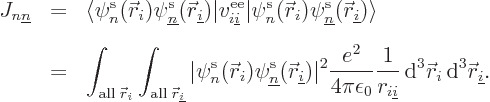
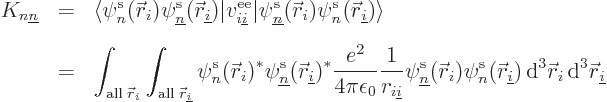
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
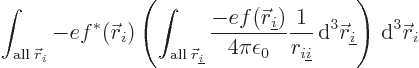
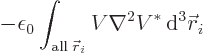
![]()
![]()
![]() ,
,