| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
D.15 The hydrogen radial wave functions
This will be child’s play for harmonic oscillator,
{D.12}, and spherical harmonics,
{D.14}, veterans. If you replace the angular terms in
(4.33) by 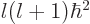 , and then divide the entire
equation by
, and then divide the entire
equation by 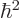 , you get
, you get
Since 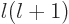 is nondimensional, all terms in this equation must
be. In particular, the ratio in the third term must be the reciprocal
of a constant with the dimensions of length; so, define the
constant to be the Bohr radius
is nondimensional, all terms in this equation must
be. In particular, the ratio in the third term must be the reciprocal
of a constant with the dimensions of length; so, define the
constant to be the Bohr radius 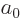 . It is convenient to also
define a correspondingly nondimensionalized radial coordinate as
. It is convenient to also
define a correspondingly nondimensionalized radial coordinate as
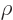

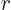

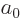 . The final term in the equation must
be nondimensional too, and that means that the energy
. The final term in the equation must
be nondimensional too, and that means that the energy  must take
the form
must take
the form 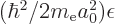 , where
, where 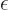 is a
nondimensional energy. In terms of these scaled coordinates you get
is a
nondimensional energy. In terms of these scaled coordinates you get
or written out
where the primes denote derivatives with respect to 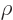 .
.
Similar to the case of the harmonic oscillator, you must have
solutions that become zero at large distances 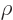 from the nucleus:
from the nucleus:
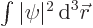 gives the probability of finding the particle
integrated over all possible positions, and if
gives the probability of finding the particle
integrated over all possible positions, and if 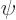 does not become
zero sufficiently rapidly at large
does not become
zero sufficiently rapidly at large 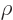 , this integral would
become infinite, rather than one (certainty) as it should. Now the
ODE above becomes for large
, this integral would
become infinite, rather than one (certainty) as it should. Now the
ODE above becomes for large 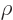 approximately
approximately 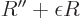
 0, which has solutions of the rough form
0, which has solutions of the rough form
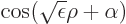 for positive
for positive 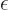 that do not
have the required decay to zero. Zero scaled energy
that do not
have the required decay to zero. Zero scaled energy 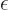 is
still too much, as can be checked by solving in terms of Bessel
functions, so you must have that
is
still too much, as can be checked by solving in terms of Bessel
functions, so you must have that 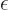 is negative. In classical
terms, the earth can only hold onto the moon since the moon’s
total energy is less than the potential energy far from the earth; if
it was not, the moon would escape.
is negative. In classical
terms, the earth can only hold onto the moon since the moon’s
total energy is less than the potential energy far from the earth; if
it was not, the moon would escape.
Anyway, for bound states, you must have the scaled energy 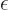 negative. In that case, the solution at large
negative. In that case, the solution at large 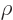 takes the
approximate form
takes the
approximate form 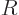
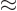
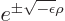 . Only
the negative sign is acceptable. You can make things a lot easier for
yourself if you peek at the final solution and rewrite
. Only
the negative sign is acceptable. You can make things a lot easier for
yourself if you peek at the final solution and rewrite 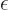 as
being
as
being  1
1
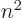 (that is not really cheating, since you are not at
this time claiming that
(that is not really cheating, since you are not at
this time claiming that  is an integer, just a positive number.)
In that case, the acceptable exponential behavior at large distance
takes the form
is an integer, just a positive number.)
In that case, the acceptable exponential behavior at large distance
takes the form 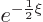 where
where 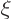

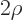

 .
Split off this exponential part by writing
.
Split off this exponential part by writing 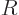

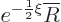 where
where 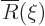 must remain
bounded at large
must remain
bounded at large 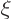 . Substituting these new variables, the
ODE becomes
. Substituting these new variables, the
ODE becomes
where the primes indicate derivatives with respect to 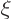 .
.
If you do a power series solution of this ODE, you see that it must
start with either power 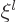 or with power
or with power 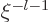 . The
latter is not acceptable, since it would correspond to an infinite
expectation value of energy. You could now expand the solution
further in powers of
. The
latter is not acceptable, since it would correspond to an infinite
expectation value of energy. You could now expand the solution
further in powers of 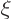 , but the problem is that tabulated
polynomials usually do not start with a power
, but the problem is that tabulated
polynomials usually do not start with a power 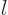 but with power zero
or one. So you would not easily recognize the polynomial you get.
Therefore it is best to split off the leading power by defining
but with power zero
or one. So you would not easily recognize the polynomial you get.
Therefore it is best to split off the leading power by defining
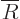

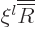 , which turns
the ODE into
, which turns
the ODE into
Substituting in a power series 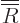

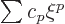 , you get
, you get
The acceptable lowest power 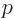 of
of 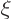 is now zero. Again the
series must terminate, otherwise the solution would behave as
is now zero. Again the
series must terminate, otherwise the solution would behave as
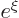 at large distance, which is unacceptable. Termination at a
highest power
at large distance, which is unacceptable. Termination at a
highest power 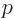

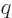 requires that
requires that  equals
equals 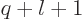 .
Since
.
Since 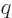 and
and 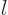 are integers, so must be
are integers, so must be  , and since the
final power
, and since the
final power 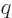 is at least zero,
is at least zero,  is at least
is at least 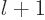 . The
correct scaled energy
. The
correct scaled energy 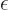

 1
1
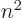 with
with 
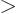
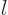 has been obtained.
has been obtained.
With  identified, you can identify the ODE as Laguerre's associated
differential equation, e.g. [41, 30.26], the
identified, you can identify the ODE as Laguerre's associated
differential equation, e.g. [41, 30.26], the
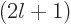 -th derivative of Laguerre's differential equation,
e.g. [41, 30.1], and the polynomial solutions as the
associated Laguerre polynomials
-th derivative of Laguerre's differential equation,
e.g. [41, 30.1], and the polynomial solutions as the
associated Laguerre polynomials 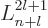 ,
e.g. [41, 30.27], the
,
e.g. [41, 30.27], the 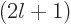 -th derivatives of
the Laguerre's polynomials
-th derivatives of
the Laguerre's polynomials 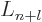 ,
e.g. [41, 30.2]. To normalize the wave function use an
integral from a table book, e.g. [41, 30.46].
,
e.g. [41, 30.2]. To normalize the wave function use an
integral from a table book, e.g. [41, 30.46].
Putting it all together, the generic expression for hydrogen eigenfunctions
are, drums please:
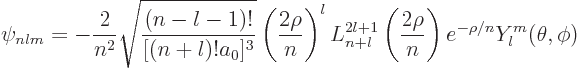 |
(D.8) |
The properties of the associated Laguerre polynomials
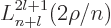 are in table books like
[41, pp. 169-172], and the spherical harmonics were
given earlier in chapter 4.2.3 and in derivation
{D.14}, (D.5).
are in table books like
[41, pp. 169-172], and the spherical harmonics were
given earlier in chapter 4.2.3 and in derivation
{D.14}, (D.5).
Do keep in mind that different references have contradictory
definitions of the associated Laguerre polynomials. This book follows
the notations of [41, pp. 169-172], who define
In other words, 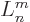 is simply the
is simply the 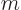 -th derivative of
-th derivative of
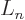 , which certainly tends to simplify things. According to
[25, p. 152], the
, which certainly tends to simplify things. According to
[25, p. 152], the most nearly standard
notation defines
Combine the messy definition of the spherical harmonics
(D.5) with the uncertain definition of the Laguerre
polynomials in the formulae (D.8) for the hydrogen energy
eigenfunctions 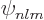 above, and there is of course always a
possibility of getting an eigenfunction wrong if you are not careful.
above, and there is of course always a
possibility of getting an eigenfunction wrong if you are not careful.
Sometimes the value of the wave functions at the origin is needed.
Now from the above solution (D.8), it is seen that
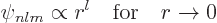 |
(D.9) |
so only the eigenfunctions 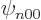 are nonzero at the origin. To
find the value requires
are nonzero at the origin. To
find the value requires 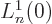 where
where 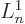 is the derivative of
the Laguerre polynomial
is the derivative of
the Laguerre polynomial 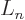 . Skimming through table books,
you can find that
. Skimming through table books,
you can find that 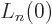

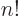 ,
[41, 30.19], while the differential equation for these
function implies that
,
[41, 30.19], while the differential equation for these
function implies that 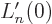

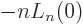 . Therefore:
. Therefore:
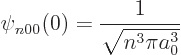 |
(D.10) |
![]() ,
,![]() ,
,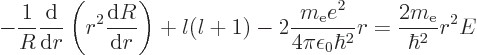
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]() ,
,![]()
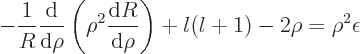
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]() 1
1![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.![]()
![]() .
.![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]() -
-![]() ,
,![]() -
-![]() ,
,![]()