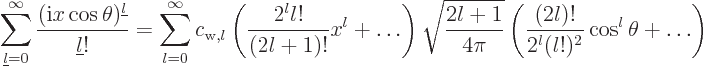| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
Subsections
D.16 Constant spherical potentials derivations
This note gives the derivations for constant potentials in spherical
coordinates.
D.16.1 The eigenfunctions
The derivation of the given spherical eigenfunction is almost comically
trivial compared to similar problems in quantum mechanics.
Following the lines of the hydrogen atom derivation, chapter
4.3.2, the radial functions 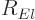 are found to satisfy the
equation
are found to satisfy the
equation
To clean this up a bit more, define new dependent and independent
variables. In particular, set 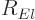

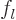 and
and 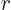

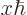

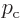 . That produces the spherical Bessel
equation
. That produces the spherical Bessel
equation
It is now to be shown that the solutions 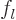 to this equation are
the Hankel and Bessel functions as given earlier.
to this equation are
the Hankel and Bessel functions as given earlier.
To do so, make another change of dependent variable by setting 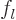

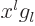 . That gives for the
. That gives for the 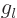 :
:
Check, by simply plugging it in, that 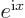

 is a solution for
is a solution for
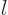
 0.
0.
Now make a further change in independent variable from  to
to
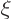

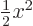 to give
to give
Note that the equation for 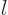
 1 is obtained by differentiating
the one for
1 is obtained by differentiating
the one for 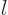
 0, (taking
0, (taking 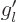 as the new unknown.). That
implies that the
as the new unknown.). That
implies that the 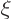 -derivative of the solution for
-derivative of the solution for 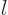
 0 above is a solution for
0 above is a solution for 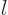
 1. Keep differentiating to get
solutions for all values of
1. Keep differentiating to get
solutions for all values of 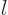 . That produces the spherical
Hankel functions of the first kind; the remaining constant is just an
arbitrarily chosen normalization factor.
. That produces the spherical
Hankel functions of the first kind; the remaining constant is just an
arbitrarily chosen normalization factor.
Since the original differential equation is real, the real and
imaginary parts of these Hankel functions, as well as their complex
conjugates, must be solutions too. That gives the spherical Bessel
functions and Hankel functions of the second kind, respectively.
Note that all of them are just finite sums of elementary
functions. And that physicists do not even disagree over their
definition, just their names.
D.16.2 The Rayleigh formula
To derive the Rayleigh formula, convert the linear momentum
eigenfunction to spherical coordinates by setting 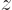

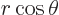 . Also, for brevity set
. Also, for brevity set 

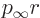

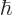 . That turns the linear momentum
eigenfunction into
. That turns the linear momentum
eigenfunction into
the latter from Taylor series expansion of the exponential.
Now this is an energy eigenfunction. It can be written in terms of
the spherical eigenfunctions
with the same energy because the 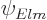 are complete. In
addition, the only eigenfunctions needed are those with
are complete. In
addition, the only eigenfunctions needed are those with 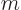
 0.
The reason is that the spherical harmonics
0.
The reason is that the spherical harmonics 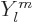 are simply Fourier
modes in the
are simply Fourier
modes in the 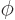 direction, {D.14}
(D.5), and the linear momentum eigenfunction above does
not depend on
direction, {D.14}
(D.5), and the linear momentum eigenfunction above does
not depend on 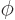 . Therefore
. Therefore
for suitable coefficients 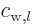 .
.
To find these coefficients, find the lowest power of  in
in 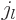 by
writing the sine in (A.19) as a Taylor series and then
switching to
by
writing the sine in (A.19) as a Taylor series and then
switching to 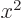 as independent variable. Similarly, find the
highest power of
as independent variable. Similarly, find the
highest power of 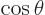 in
in 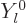 , {D.14}
(D.5), by looking up the Rodrigue’s formula for the
Legendre polynomial appearing in it. That gives
, {D.14}
(D.5), by looking up the Rodrigue’s formula for the
Legendre polynomial appearing in it. That gives
Each coefficient 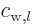 must be chosen to match the term
with
must be chosen to match the term
with 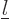

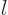 in the first sum, because the terms for the other values
for
in the first sum, because the terms for the other values
for 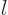 do not have a low enough power of
do not have a low enough power of  or a high enough power
of the cosine. That gives the Rayleigh values of the coefficients as
listed earlier.
or a high enough power
of the cosine. That gives the Rayleigh values of the coefficients as
listed earlier.
![]()
![\begin{displaymath}
\frac{{\rm d}}{{\rm d}r} \left(r^2 \frac{{\rm d}R_{El}}{{\r...
...ft[\frac{p_{\rm {c}}^2}{\hbar^2}r^2 - l(l+1)\right] R_{El} = 0
\end{displaymath}](img6151.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![\begin{displaymath}
\frac{{\rm d}}{{\rm d}x}\left(x^2\frac{{\rm d}f_l}{{\rm d}x}\right)
+ \left[x^2 - l(l+1)\right] f_l = 0
\end{displaymath}](img6154.gif)
![]()
![]()
![]() .
.![]() :
:![]()
![]()
![]()
![]()
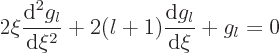
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() .
.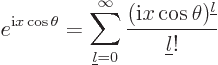
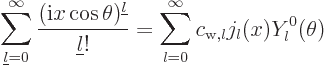
![]()
![]()
![]()
![]()
![]() ,
,