| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.5 The reduced mass
Two-body systems, like the earth-moon system of celestial mechanics or
the proton-electron hydrogen atom of quantum mechanics, can be
analyzed more simply using reduced mass. In this note both a
classical and a quantum derivation will be given. The quantum
derivation will need to anticipate some results on multi-particle
systems from chapter 5.1.
In two-body systems the two bodies move around their combined center
of gravity. However, in examples such as the ones mentioned, one body
is much more massive than the other. In that case the center of
gravity almost coincides with the heavy body, (earth or proton).
Therefore, in a naive first approximation it may be assumed that the
heavy body is at rest and that the lighter one moves around it. It
turns out that this naive approximation can be made exact by replacing
the mass of the lighter body by an reduced mass. That simplifies the
mathematics greatly by reducing the two-body problem to that of a
single one. Also, it now produces the exact answer regardless of the
ratio of masses involved.
The classical derivation is first. Let 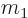 and
and 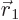 be the mass
and position of the massive body (earth or proton), and
be the mass
and position of the massive body (earth or proton), and 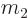 and
and
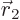 those of the lighter one (moon or electron). Classically the
force
those of the lighter one (moon or electron). Classically the
force 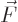 between the masses will be a function of the
difference
between the masses will be a function of the
difference 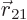

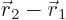 in their positions. In the
naive approach the heavy mass is assumed to be at rest at the origin.
Then
in their positions. In the
naive approach the heavy mass is assumed to be at rest at the origin.
Then 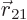

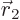 , and so the naive equation of
motion for the lighter mass is, according to Newton’s second law,
, and so the naive equation of
motion for the lighter mass is, according to Newton’s second law,
Now consider the true motion. The center of gravity is defined as a
mass-weighted average of the positions of the two masses:
It is shown in basic physics that the net external force on the system
equals the total mass times the acceleration of the center of gravity.
Since in this case it will be assumed that there are no external
forces, the center of gravity moves at a constant velocity. Therefore,
the center of gravity can be taken as the origin of an inertial
coordinate system. In that coordinate system, the positions of the
two masses are given by
because the position 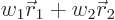 of the center of gravity must
be zero in this system, and the difference
of the center of gravity must
be zero in this system, and the difference 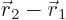 must be
must be
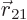 . (Note that the sum of the two weight factors is
one.) Solve these two equations for
. (Note that the sum of the two weight factors is
one.) Solve these two equations for 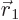 and
and 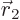 and you get
the result above.
and you get
the result above.
The true equation of motion for the lighter body is 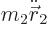

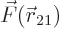 , or plugging in the above expression
for
, or plugging in the above expression
for 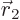 in the center of gravity system,
in the center of gravity system,
That is exactly the naive equation of motion if you replace 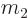 in
it by the reduced mass
in
it by the reduced mass 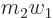 , i.e. by
, i.e. by
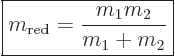 |
(A.16) |
The reduced mass is almost the same as the lighter mass if the
difference between the masses is large, like it is in the cited
examples, because then 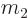 can be ignored compared to
can be ignored compared to 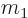 in the
denominator.
in the
denominator.
The bottom line is that the motion of the two-body system consists of
the motion of its center of gravity plus motion around its center of
gravity. The motion around the center of gravity can be described in
terms of a single reduced mass moving around a fixed center.
The next question is if this reduced mass idea is still valid in
quantum mechanics. Quantum mechanics is in terms of a wave function
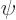 that for a two-particle system is a function of both
that for a two-particle system is a function of both 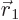 and
and 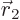 . Also, quantum mechanics uses the potential
. Also, quantum mechanics uses the potential
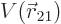 instead of the force. The Hamiltonian eigenvalue
problem for the two particles is:
instead of the force. The Hamiltonian eigenvalue
problem for the two particles is:
where the two kinetic energy Laplacians in the Hamiltonian 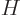 are
with respect to the position coordinates of the two particles:
are
with respect to the position coordinates of the two particles:
Now make a change of variables from 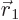 and
and 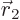 to
to
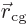 and
and 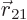 where
where
The derivatives of 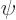 can be converted using the chain rule of
differentiation:
can be converted using the chain rule of
differentiation:
or differentiating once more and summing
and a similar expression for 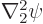 , but with
, but with 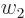 instead of
instead of 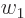 and a plus sign instead of the minus sign. Combining
them together in the Hamiltonian, and substituting for
and a plus sign instead of the minus sign. Combining
them together in the Hamiltonian, and substituting for 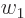 and
and
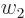 , the mixed derivatives drop out against each other and
what is left is
, the mixed derivatives drop out against each other and
what is left is
The first term is the kinetic energy that the total mass would have if
it was at the center of gravity; the next two terms are kinetic and
potential energy around the center of gravity, in terms of the
distance between the masses and the reduced mass.
The Hamiltonian eigenvalue problem 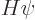

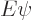 has separation of
variables solutions of the form
has separation of
variables solutions of the form
Substituting this and the Hamiltonian above into 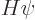

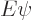 and
dividing by
and
dividing by 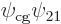 produces
produces
Call the first term in the left hand side 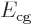 and the second
and the second
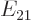 . By that definition,
. By that definition, 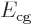 would normally be a
function of
would normally be a
function of 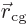 , because
, because 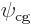 is, but
since it is equal to
is, but
since it is equal to 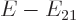 and those do not depend on
and those do not depend on
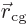 ,
, 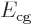 cannot either, and must be a
constant. By similar reasoning,
cannot either, and must be a
constant. By similar reasoning, 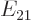 cannot depend on
cannot depend on 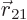 and must be a constant too. Therefore, rewriting the definitions of
and must be a constant too. Therefore, rewriting the definitions of
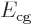 and
and 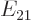 , two separate eigenvalue problems are
obtained:
, two separate eigenvalue problems are
obtained:
The first describes the quantum mechanics of an imaginary total mass
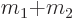 located at the center of gravity. The second describes an
imaginary reduced mass
located at the center of gravity. The second describes an
imaginary reduced mass 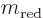 at a location
at a location 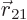 away
from a fixed center that experiences a potential
away
from a fixed center that experiences a potential 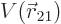 .
.
For the hydrogen atom, it means that if the problem with a stationary
proton is solved using an reduced electron mass
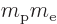

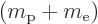 , it solves the true problem in which the
proton moves a bit too. Like in the classical analysis, the quantum
analysis shows that in addition the atom can move as a unit, with a
motion described in terms of its center of gravity.
, it solves the true problem in which the
proton moves a bit too. Like in the classical analysis, the quantum
analysis shows that in addition the atom can move as a unit, with a
motion described in terms of its center of gravity.
It can also be concluded, from a slight generalization of the quantum
analysis, that a constant external gravity field, like that of the sun
on the earth-moon system, or of the earth on a hydrogen atom, causes
the center of gravity to accelerate correspondingly, but does not
affect the motion around the center of gravity at all. That reflects
a basic tenet of general relativity.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]()
![]() .
.![]()
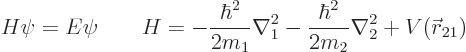
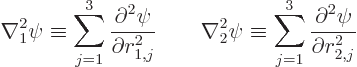
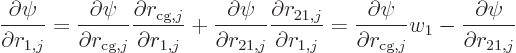
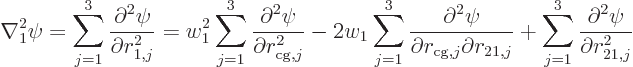
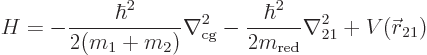
![]()
![]()
![]()
![\begin{displaymath}
- \frac{\hbar^2}{2(m_1+m_2)} \frac{1}{\psi_{\rm cg}}
\nabl...
...\hbar^2}{2 m_{\rm red}} \nabla^2_{21} + V\right]\psi_{21}
= E
\end{displaymath}](img3706.gif)
![\begin{displaymath}
- \frac{\hbar^2}{2(m_1+m_2)}\nabla^2_{\rm cg}\psi_{\rm cg}
...
...rm red}} \nabla^2_{21} + V\right]\psi_{21}
= E_{21} \psi_{21}
\end{displaymath}](img3710.gif)
![]()
![]()
![]() ,
,