5.1 Wave Func­tion for Mul­ti­ple Par­ti­cles

While a sin­gle par­ti­cle is de­scribed by a wave func­tion $\Psi({\skew0\vec r};t)$, a sys­tem of two par­ti­cles, call them 1 and 2, is de­scribed by a wave func­tion

$$\Psi({\skew0\vec r}_1,{\skew0\vec r}_2;t)$$ (5.1)

de­pend­ing on both par­ti­cle po­si­tions. The value of $\vert\Psi({\skew0\vec r}_1,{\skew0\vec r}_2;t)\vert^2{ \rm d}^3{\skew0\vec r}_1{ \rm d}^3{\skew0\vec r}_2$ gives the prob­a­bil­ity of si­mul­ta­ne­ously find­ing par­ti­cle 1 within a vicin­ity ${ \rm d}^3{\skew0\vec r}_1$ of ${\skew0\vec r}_1$ and par­ti­cle 2 within a vicin­ity ${ \rm d}^3{\skew0\vec r}_2$ of ${\skew0\vec r}_2$.

The wave func­tion must be nor­mal­ized to ex­press that the elec­trons must be some­where:

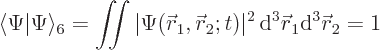$$\langle \Psi \vert \Psi \rangle_6 = \mathop{\int\kern-7pt\... ...rt^2{ \rm d}^3 {\skew0\vec r}_1{\rm d}^3 {\skew0\vec r}_2 = 1$$ (5.2)

where the sub­script 6 of the in­ner prod­uct is just a re­minder that the in­te­gra­tion is over all six scalar po­si­tion co­or­di­nates of $\Psi$.

The un­der­ly­ing idea of in­creas­ing sys­tem size is “every pos­si­ble com­bi­na­tion:” al­low for every pos­si­ble com­bi­na­tion of state for par­ti­cle 1 and state for par­ti­cle 2. For ex­am­ple, in one di­men­sion, all pos­si­ble $x$ po­si­tions of par­ti­cle 1 geo­met­ri­cally form an $x_1$-​axis. Sim­i­larly all pos­si­ble $x$ po­si­tions of par­ti­cle 2 form an $x_2$-​axis. If every pos­si­ble po­si­tion $x_1$ is sep­a­rately com­bined with every pos­si­ble po­si­tion $x_2$, the re­sult is an $x_1,x_2$-​plane of pos­si­ble po­si­tions of the com­bined sys­tem.

Sim­i­larly, in three di­men­sions the three-di­men­sion­al space of po­si­tions ${\skew0\vec r}_1$ com­bines with the three-di­men­sion­al space of po­si­tions ${\skew0\vec r}_2$ into a six-di­men­sion­al space hav­ing all pos­si­ble com­bi­na­tions of val­ues for ${\skew0\vec r}_1$ with all pos­si­ble val­ues for ${\skew0\vec r}_2$.

The in­crease in the num­ber of di­men­sions when the sys­tem size in­creases is a ma­jor prac­ti­cal prob­lem for quan­tum me­chan­ics. For ex­am­ple, a sin­gle ar­senic atom has 33 elec­trons, and each elec­tron has 3 po­si­tion co­or­di­nates. It fol­lows that the wave func­tion is a func­tion of 99 scalar vari­ables. (Not even count­ing the nu­cleus, spin, etcetera.) In a brute-force nu­mer­i­cal so­lu­tion of the wave func­tion, maybe you could re­strict each po­si­tion co­or­di­nate to only ten com­pu­ta­tional val­ues, if no very high ac­cu­racy is de­sired. Even then, $\Psi$ val­ues at 10$\POW9,{99}$ dif­fer­ent com­bined po­si­tions must be stored, re­quir­ing maybe 10$\POW9,{91}$ Gi­ga­bytes of stor­age. To do a sin­gle mul­ti­pli­ca­tion on each of those those num­bers within a few years would re­quire a com­puter with a speed of 10$\POW9,{82}$ gi­gaflops. No need to take any of that ar­senic to be long dead be­fore an an­swer is ob­tained. (Imag­ine what it would take to com­pute a mi­cro­gram of ar­senic in­stead of an atom.) Ob­vi­ously, more clever nu­mer­i­cal pro­ce­dures are needed.

Some­times the prob­lem size can be re­duced. In par­tic­u­lar, the prob­lem for a two-par­ti­cle sys­tem like the pro­ton-elec­tron hy­dro­gen atom can be re­duced to that of a sin­gle par­ti­cle us­ing the con­cept of re­duced mass. That is shown in ad­den­dum {A.5}.

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

To de­scribe mul­ti­ple-par­ti­cle sys­tems, just keep adding more in­de­pen­dent vari­ables to the wave func­tion.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Un­for­tu­nately, this makes many-par­ti­cle prob­lems im­pos­si­ble to solve by brute force.

5.1 Re­view Ques­tions

1.

A sim­ple form that a six-di­men­sion­al wave func­tion can take is a prod­uct of two three-di­men­sion­al ones, as in $\psi({\skew0\vec r}_1,{\skew0\vec r}_2)$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\psi_1({\skew0\vec r}_1)\psi_2({\skew0\vec r}_2)$. Show that if $\psi_1$ and $\psi_2$ are nor­mal­ized, then so is $\psi$.

So­lu­tion com­plex-a

2.

Show that for a sim­ple prod­uct wave func­tion as in the pre­vi­ous ques­tion, the rel­a­tive prob­a­bil­i­ties of find­ing par­ti­cle 1 near a po­si­tion ${\skew0\vec r}_a$ ver­sus find­ing it near an­other po­si­tion ${\skew0\vec r}_b$ is the same re­gard­less where par­ti­cle 2 is. (Or rather, where par­ti­cle 2 is likely to be found.)

Note: This is the rea­son that a sim­ple prod­uct wave func­tion is called un­cor­re­lated. For par­ti­cles that in­ter­act with each other, an un­cor­re­lated wave func­tion is of­ten not a good ap­prox­i­ma­tion. For ex­am­ple, two elec­trons re­pel each other. All else be­ing the same, the elec­trons would rather be at po­si­tions where the other elec­tron is nowhere close. As a re­sult, it re­ally makes a dif­fer­ence for elec­tron 1 where elec­tron 2 is likely to be and vice-versa. To han­dle such sit­u­a­tions, usu­ally sums of prod­uct wave func­tions are used. How­ever, for some cases, like for the he­lium atom, a sin­gle prod­uct wave func­tion is a per­fectly ac­cept­able first ap­prox­i­ma­tion. Real-life elec­trons are crowded to­gether around at­tract­ing nu­clei and learn to live with each other.

So­lu­tion com­plex-b