|
|
|
|
|
Next: 5.3 Two-State Systems |
|
This section uses similar approximations as for the hydrogen molecular
ion of chapter 4.6 to examine the neutral ![]()
Of course, share
is a vague term, but the discussion
will show what it really means in terms of the six-dimensional
electron wave function.
Just like for the hydrogen molecular ion of chapter 4.6,
for the neutral molecule the Born-Oppenheimer approximation will
be made that the protons are at given fixed points. So the problem
simplifies to just finding the wave function of the two electrons,
![]() ,
,![]()
![]()
![]() .
.
In the Hamiltonian, following the Newtonian analogy the kinetic and
potential energy operators simply add:
In this expression, the Laplacians of the first two, kinetic energy,
terms are with respect to the position coordinates of the two
electrons:
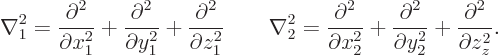
Key Points
- The Hamiltonian for the 6-dimensional electron wave function has been written down.
Verify that the repulsive potential between the electrons is infinitely large when the electrons are at the same position.
Note: You might therefore think that the wave function needs to be zero at the locations in six-dimensional space where ![]()
![]()
![]() .
.Coulomb hole.” But the truth is that in quantum mechanics, electrons are smeared out due to uncertainty. That causes electron 1 to “see electron 2 at all sides
, and vice-versa, and they do therefore not encounter any unusually large potential when the wave function is nonzero at ![]()
![]()
![]() .
.
Note that the total kinetic energy term is simply a multiple of the six-dimensional Laplacian operator. It treats all Cartesian position coordinates exactly the same, regardless of which direction or which electron it is. Is this still the case if other particles are involved?
The next step is to identify an approximate ground state for the hydrogen molecule. Following the same approach as in chapter 4.6, it will first be assumed that the protons are relatively far apart. One obvious approximate solution is then that of two neutral atoms, say the one in which electron 1 is around the left proton in its ground state and electron 2 is around the right one.
To formulate the wave function for that, the shorthand notation
![]()
![]()
The wave function that describes that electron 1 is in the ground
state around the left proton and electron 2 around the right one will
be approximated to be the product of the single electron states:
Taking the combined wave function as a product of single electron
states is really equivalent to an assumption that the two electrons
are independent. Indeed, for the product state, the probability of
finding electron 1 at position ![]()
![]()
![\begin{displaymath}
\begin{array}{l}
\mbox{[probability of finding 1 at ${\ske...
... at ${\skew0\vec r}_2$ unaffected by where 1 is]}
\end{array}\end{displaymath}](img917.gif)
Key Points
- When the protons are well apart, an approximate ground state is that of two neutral atoms.
- Single electron wave functions for that case are
and .
- The complete wave function for that case is
assuming that electron 1 is around the left proton and electron 2 around the right one. ,
If electron 2 does not affect where electron 1 is likely to be, how would a grey-scale picture of the probability of finding electron 1 look?
When the protons are close to each other, the electrons do affect each other, and the wave function above is no longer valid. But suppose you were given the true wave function, and you were once again asked to draw the blob showing the probability of finding electron 1 (using a plotting package, say). What would the big problem be?
For multiple-particle systems like the electrons of the hydrogen
molecule, showing the magnitude of the wave function as grey tones no
longer works since it is a function in six-dimensional space. You cannot
visualize six-dimensional space. However, at every spatial position ![]()
![]() ,
,![]()
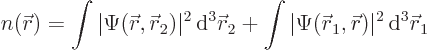 |
(5.4) |
The probability density ![]()
![]()
![]()
Key Points
- The probability density is the probability per unit volume of finding an electron, whichever one, near a given point.
Suppose, given the wave function ![]() ,
,
This section will examine the states where the protons share the two electrons.
The first thing is to shorten the notations a bit. So, the state
![]()
![]() ,
,![]() ,
,![]() .
.![]() ;
;
The every possible combination
idea of combining every
possible state for electron 1 with every possible state for electron 2
would suggest that the states ![]()
![]()
States where the electrons are no longer assigned to a particular
proton can be found as linear combinations of
![]()
![]() :
:
| (5.5) |
The eigenfunction must be normalized, which noting that ![]()
![]()
| (5.6) |
| (5.7) |
The most important combination state is the one with ![]()
![]()
![]() :
:
| (5.8) |
The probability density of this wave function looks like figure 5.2. It has increased likelihood for electrons to be found in between the protons, compared to figure 5.1 in which each proton had its own electron.
The state with ![]()
![]()
![]()
![]() ,
,
| (5.10) |
antisymmetricwith respect to exchanging electron 1 with electron 2: swapping
Key Points
- In state
the electron numbered 1 is around the left proton and 2 around the right one. ,
- In state
the electron numbered 1 is around the right proton and 2 around the left one. ,
- In the symmetric state
the protons share the electrons equally; each electron has an equal chance of being found around either proton. In this state there is increased probability of finding an electron somewhere in between the protons.
- In the antisymmetric state
the protons also share the electrons equally; each electron has again an equal chance of being found around either proton. But in this state there is decreased probability of finding an electron somewhere in between the protons.
- So, like for the molecular ion, at large proton separations the weird trick of shuffling unobservable wave functions around does again produce different physical states with pretty much the same energy.
Obviously, the visual difference between the various states is minor. It may even seem counter-intuitive that there is any difference at all: the states ![]()
![]()
The quantum difference would be much more clear if you could see the full six-dimensional wave function, but visualizing six-dimensional space just does not work. However, if you restrict yourself to only looking on the ![]() -
-![]() -
-![]()
![]() ?
?
Try to guess these probabilities in the ![]() -
-
Based on the previous question, how would you think the probability density ![]()
The purpose of this section is to find an approximation to the ground state of the hydrogen molecule using the rough approximation of the wave function described in the previous subsections.
Like for the hydrogen molecular ion of chapter 4.6.6, the
idea is that since the true ground state is the state of lowest energy
among all wave functions, the best among approximate wave
functions is the one with the lowest energy. The approximate wave
functions are here of the form
![]() ;
;
A computer program is again needed to print out the expectation value
of the energy for various values of the ratio of coefficients ![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
You might just want to take it on faith that the binding energy, at
the state of lowest energy found, turns out to be 3.2 eV, at a proton
to proton spacing of 0.87 Å, and that it occurs for the symmetric
state ![]()
![]()
![]() .
.
Key Points
- An approximate ground state can be found for the hydrogen molecule using a variational method much like that for the molecular ion.
The solution for the ground state of the hydrogen molecule obtained in the previous subsection is, like the one for the molecular ion, pretty good. The approximate binding energy, 3.2 eV, is not too much different from the experimental value of 4.52 eV. Similarly, the bond length of 0.87 Å is not too far from the experimental value of 0.74 Å.
Qualitatively, the exact ground state wave function is real, positive and symmetric with respect to reflection around the symmetry plane and to rotations around the line connecting the protons, and so is the approximate one. The reasons for these properties are similar as for the molecular ion; {A.8,A.9}.
One very important new symmetry for the neutral molecule is the effect
of exchanging the electrons, replacing ![]()
![]()
One issue that does not occur for the molecular ion, but only for the neutral molecule is the mutual repulsion between the two electrons. This repulsion is reduced when the electron clouds start to merge, compared to what it would be if the clouds were more compact. (A similar effect is that the gravity force of the earth decreases when you go down below the surface. To be sure, the potential energy keeps going down, or up for electron clouds, but not as much as it would otherwise. Compare figure 13.7.) Since the nuclei are compact, it gives an advantage to nucleus-electron attraction over electron-electron repulsion. This increases the binding energy significantly; in the approximate model from about 1.8 eV to 3.2 eV. It also allows the protons to approach more closely; {D.23}.
The question has been asked whether there should not be an “activation energy” involved in creating the hydrogen molecule from the hydrogen atoms. The answer is no, hydrogen atoms are radicals, not stable molecules that need to be taken apart before recombining. In fact, the hydrogen atoms attract each other even at large distances due to Van der Waals attraction, chapter 10.1, an effect lost in the approximate wave functions used in this section. But hydrogen atoms that fly into each other also have enough energy to fly apart again; some of the excess energy must be absorbed elsewhere to form a stable molecule. According to web sources, hydrogen molecule formation in the universe is believed to typically occur on dust specks.
Key Points
- The approximate ground state is pretty good, considering its simplicity.