|
|
|
|
|
Next: 11.11 The Big Lie of Distinguishable Particles |
|
With the cleverest inventors and the greatest scientists relentlessly
trying to fool nature and circumvent the second law, how come nature
never once gets confused, not even by the most complicated,
convoluted, unusual, ingenious schemes? Nature does not outwit them
by out-thinking them, but by maintaining an accounting system that
cannot be fooled. Unlike human accounting systems, this accounting
system does not assign a monetary value to each physical system, but a
measure of messiness called entropy.
Then, in any
transaction within or between systems, nature simply makes sure that
this entropy is not being reduced; whatever entropy one system gives
up must always be less than what the other system receives.
So what can this numerical grade of messiness called entropy be?
Surely, it must be related somehow to the second law as stated by
Clausius and Kelvin and Planck, and to the resulting Carnot engines
that cannot be beat. Note that the Carnot engines relate heat added
to temperature. In particular an infinitesimally small Carnot engine
would take in an infinitesimal amount ![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
If ![]()
![]()
![]()
![\begin{figure}\centering
\setlength{\unitlength}{1pt}
\begin{picture}(300,11...
...1){\circle*{3}}
\put(-41,80.6){\makebox(0,0)[b]{C}}
\end{picture}
\end{figure}](img2416.gif) |
The entropy as defined above is a specific number for a system in
thermal equilibrium, just like its pressure, temperature, particle
density, and internal energy are specific numbers. You might think
that you could get a different value for the entropy by following a
different process path from the reference state to the desired state.
But the second law prevents that. To see why, consider the
pressure-volume diagram in figure 11.14. Two different
reversible processes are shown leading from the reference state to a
desired state. A bundle of reversible adiabatic process lines is also
shown; those are graphical representations of processes in which there
is no heat exchange between the system and its surroundings. The
bundle of adiabatic lines chops the two process paths into small
pieces, of almost constant temperature, that pairwise have the same
value of ![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
So what happens if the reference and final states are still the same,
but there is a slight glitch for a single segment AB, making the
process over that one segment irreversible? In that case, the heat
engine argument no longer applies, since it runs through the segment
AB in reversed order, and irreversible processes cannot be reversed.
The refrigeration cycle argument says that the amount of heat
![]()
![]()
![]()
![]()
![]() .
.
Note that the above formula is only valid if the system has an definite temperature, as in this particular example. Typically this is simply not true in irreversible processes; for example, the interior of the system might be hotter than the outside. The real importance of the above formula is to confirm that the defined entropy is indeed a measure of messiness and not of order; reversible processes merely shuffle entropy around from one system to the next, but irreversible processes increase the net entropy content in the universe.
So what about the entropy of a system that is not in thermal equilibrium? Equation (11.18) only applies for systems in thermal equilibrium. In order for nature not to become confused in its entropy accounting system, surely entropy must still have a numerical value for nonequilibrium systems. If the problem is merely temperature or pressure variations, where the system is still in approximate thermal equilibrium locally, you could just integrate the entropy per unit volume over the volume. But if the system is not in thermal equilibrium even on macroscopically small scales, it gets much more difficult. For example, air crossing a typical shock wave (sonic boom) experiences a significant increase in pressure over an extremely short distance. Better bring out the quantum mechanics trick box. Or at least molecular dynamics.
Still, some important general observations can be made without running to a computer. An “isolated” system is a system that does not interact with its surroundings in any way. Remember the example where the air inside a room was collected and neatly put inside a glass? That was an example of an isolated system. Presumably, the doors of the room were hermetically sealed. The walls of the room are stationary, so they do not perform work on the air in the room. And the air comes rushing back out of the glass so quickly that there is really no time for any heat conduction through the walls. If there is no heat conduction with the outside, then there is no entropy exchange with the outside. So the entropy of the air can only increase due to irreversible effects. And that is exactly what happens: the air exploding out of the glass is highly irreversible, (no, it has no plans to go back in), and its entropy increases rapidly. Quite quickly however, the air spreads again out over the entire room and settles down. Beyond that point, the entropy remains further constant.
An isolated system evolves to the state of maximum possible entropy and then stays there.The state of maximum possible entropy is the thermodynamically stable state a system will assume if left alone.
A more general system is an “adiabatic” or “insulated” system. Work may be performed on such a system, but there is still no heat exchange with the surroundings. That means that the entropy of such a system can again only increase due to reversibility. A simple example is a thermos bottle with a cold drink inside. If you continue shaking this thermos bottle violently, the cold drink will heat up due to its viscosity, its internal friction, and it will not stay a cold drink for long. Its entropy will increase while you are shaking it.
The entropy of adiabatic systems can only increase.But, of course, that of an open system may not. It is the recipe of life, {N.25}.
You might wonder why this book on quantum mechanics included a concise, but still very lengthy classical description of the second law. It is because the evidence for the second law is so much more convincing based on the macroscopic evidence than on the microscopic one. Macroscopically, the most complex systems can be accurately observed, microscopically, the quantum mechanics of only the most simplistic systems can be rigorously solved. And whether we can observe the solution is still another matter.
However, given the macroscopic fact that there really is an accounting measure of messiness called entropy, the question becomes what is its actual microscopic nature? Surely, it must have a relatively simple explanation in terms of the basic microscopic physics? For one, nature never seems to get confused about what it is, and for another, you really would expect something that is clearly so fundamental to nature to be relatively esthetic when expressed in terms of mathematics.
And that thought is all that is needed to guess the true microscopic nature of entropy. And guessing is good, because it gives a lot of insight why entropy is what it is. And to ensure that the final result is really correct, it can be cross checked against the macroscopic definition (11.18) and other known facts about entropy.
The first guess is about what physical microscopic quantity would be
involved. Now microscopically, a simple system is described by energy
eigenfunctions ![]() ,
,![]() ,
,
If the system is in a single eigenstate for sure, the probability
![]()
![]() ,
,![]()
![]()
![]() .
.![]() ,
,![]() .
.![]()
![]()
![]()
![]()
So try a slightly more general possibility, that the entropy is the
average of some function of the probability, as in ![]()
![]()
![]() .
.![]()
![]() ,
,
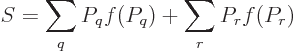
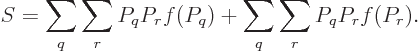
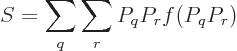
The microscopic definition of entropy has been guessed:
At absolute zero temperature, the system is in the ground state. That
means that probability ![]()
![]()
![]()
At temperatures above absolute zero, many eigenfunctions will have
nonzero probabilities. That makes the entropy positive, because
logarithms of numbers less than one are negative. (It should be noted
that ![]()
![]()
![]()
![]() .
.
To put the definition of entropy on a less abstract basis, assume that
you schematize the system of interest into unimportant eigenfunctions
that you give zero probability, and a remaining ![]()
![]() .
.![]() ,
,
The next step is to check the expression. Derivations are given in {D.60}, but here are the results. For systems in thermal equilibrium, is the entropy the same as the one given by the classical integration (11.18)? Check. Does the entropy exist even for systems that are not in thermal equilibrium? Check, quantum mechanics still applies. For a system of given energy, is the entropy smallest when the system is in a single energy eigenfunction? Check, it is zero then. For a system of given energy, is the entropy the largest when all eigenfunctions of that energy have the same probability, as the fundamental assumption of quantum statistics suggests? Check. For a system with given expectation energy but uncertainty in energy, is the entropy highest when the probabilities are given by the canonical probability distribution? Check. For two systems in thermal contact, is the entropy greatest when their temperatures have become equal? Check.
Feynman [18, p. 8] gives an argument to show that the
entropy of an isolated system always increases with time. Taking the
time derivative of (11.20),
![\begin{displaymath}
\frac{{\rm d}S}{{\rm d}t} = -k_{\rm B}\sum_q [\ln(P_q)+1] \...
...d}t}
= -k_{\rm B}\sum_q \sum_r [\ln(P_q)+1] R_{qr} [P_r-P_q],
\end{displaymath}](img2435.gif)
measurementwild card, chapter 7.6 you might consider this more a validation of time dependent perturbation theory than of the expression for entropy. Then there is the problem of ensuring that a perturbed and measured system is adiabatic.
In any case, it may be noted that the checks on the expression for entropy, as given above, cut both ways. If you accept the expression for entropy, the canonical probability distribution follows. They are consistent, and in the end, it is just a matter of which of the two postulates you are more willing to accept as true.