| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
11.11 The Big Lie of Distinguishable Particles
If you try to find the entropy of the system of distinguishable
particles that produces the Maxwell-Boltzmann distribution, you are in
for an unpleasant surprise. It just cannot be done. The problem is
that the number of eigenfunctions for 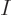 distinguishable particles is
typically roughly
distinguishable particles is
typically roughly 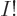 larger than for
larger than for 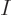 identical bosons or
fermions. If the typical number of states becomes larger by a factor
identical bosons or
fermions. If the typical number of states becomes larger by a factor
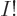 , the logarithm of the number of states increases by
, the logarithm of the number of states increases by
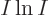 , (using the Stirling formula), which is no longer
proportional to the size of the system
, (using the Stirling formula), which is no longer
proportional to the size of the system 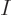 , but much larger than
that. The specific entropy would blow up with system size.
, but much larger than
that. The specific entropy would blow up with system size.
What gives? Now the truth must be revealed. The entire notion of
distinguishable particles is a blatant lie. You are simply not going
to have 10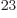 distinguishable particles in a box. Assume they
would be 10
distinguishable particles in a box. Assume they
would be 10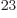 different molecules. It would a take a chemistry
handbook of 10
different molecules. It would a take a chemistry
handbook of 10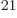 pages to list them, one line for each. Make
your system size 1 000 times as big, and the handbook gets 1 000
times thicker still. That would be really messy! When identical
bosons or fermions are far enough apart that their wave functions do
no longer overlap, the symmetrization requirements are no longer
important for most practical purposes. But if you start counting
energy eigenfunctions, as entropy does, it is a different story. Then
there is no escaping the fact that the particles really are, after
all, indistinguishable forever.
pages to list them, one line for each. Make
your system size 1 000 times as big, and the handbook gets 1 000
times thicker still. That would be really messy! When identical
bosons or fermions are far enough apart that their wave functions do
no longer overlap, the symmetrization requirements are no longer
important for most practical purposes. But if you start counting
energy eigenfunctions, as entropy does, it is a different story. Then
there is no escaping the fact that the particles really are, after
all, indistinguishable forever.
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()